tìm điều kiện xác định của biểu thức sau:
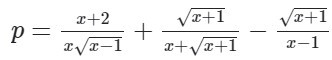
Quảng cáo
2 câu trả lời 250
Để tìm điều kiện xác định của biểu thức
\[
p = \frac{x + 2}{x \sqrt{x - 1}} + \frac{\sqrt{x + 1}}{x + \sqrt{x + 1}} - \frac{\sqrt{x + 1}}{x - 1}
\]
ta cần xét các điều kiện sau:
1. **\(x \sqrt{x - 1}\)** phải khác 0:
- \(x \neq 0\)
- \(x - 1 \geq 0 \Rightarrow x \geq 1\)
2. **\(x + \sqrt{x + 1}\)** phải khác 0:
- Từ đó, không có thêm điều kiện vì \(x + \sqrt{x + 1}\) luôn dương với mọi \(x\).
3. **\(x - 1 \neq 0\)**:
- \(x \neq 1\)
### Tóm lại:
- \(x \geq 1\)
- \(x \neq 1\)
### Điều kiện xác định:
- \(x > 1\)
Tuyệt vời! Chúng ta cùng nhau giải quyết bài toán này nhé.
Phân tích và giải quyết:
Để tìm điều kiện xác định của biểu thức P, ta cần đảm bảo rằng tất cả các biểu thức dưới dấu căn đều không âm và mẫu số của các phân thức khác 0.
1. Biểu thức dưới dấu căn không âm:
√(x-1): Để biểu thức này có nghĩa thì x - 1 ≥ 0 ⇒ x ≥ 1.
√x: Tương tự, x ≥ 0.
2. Mẫu số khác 0:
x√(x-1): Để mẫu số này khác 0 thì x ≠ 0 và x ≠ 1.
x + √x + 1: Biểu thức này luôn dương với mọi x ≥ 0 nên không cần điều kiện.
x - 1: Đã có điều kiện x ≠ 1 ở trên.
Kết hợp các điều kiện:
Từ các điều kiện trên, ta thấy rằng để biểu thức P xác định thì:
x ≥ 1 (để cả √(x-1) và √x có nghĩa)
x ≠ 0 (để mẫu số x√(x-1) khác 0)
x ≠ 1 (để mẫu số x√(x-1) và x - 1 khác 0)
Vậy điều kiện xác định của biểu thức P là x > 1.
Kết luận:
Để biểu thức P = (x+2) / (x√(x-1)) + √(x+1) / (x+√x+1) - √(x+1) / (x-1) có nghĩa thì x phải lớn hơn 1.
Lưu ý:
Điều kiện x > 1 đảm bảo rằng tất cả các biểu thức trong P đều có nghĩa và không gây ra bất kỳ vấn đề gì về toán học.
Việc tìm điều kiện xác định là một bước rất quan trọng khi giải các bài toán liên quan đến căn thức và phân thức. Nó giúp chúng ta tránh được những kết quả sai hoặc vô nghĩa.
Nguồn: DapHoi.Com
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103992
Đã trả lời bởi chuyên gia
103992 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69088
Đã trả lời bởi chuyên gia
69088 -
 Đã trả lời bởi chuyên gia
56995
Đã trả lời bởi chuyên gia
56995 -
 Đã trả lời bởi chuyên gia
47741
Đã trả lời bởi chuyên gia
47741 -
 Đã trả lời bởi chuyên gia
44729
Đã trả lời bởi chuyên gia
44729 -
 Đã trả lời bởi chuyên gia
37050
Đã trả lời bởi chuyên gia
37050 -
 Đã trả lời bởi chuyên gia
35840
Đã trả lời bởi chuyên gia
35840


