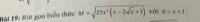Để rút gọn biểu thức \( M = \sqrt{25x^2 \cdot (x - 2\sqrt{x} + 1)} \) với điều kiện \( 0 < x < 1 \), chúng ta thực hiện các bước sau:

### Bước 1: Phân tích biểu thức bên trong dấu căn

Biểu thức bên trong dấu căn là \( 25x^2 \cdot (x - 2\sqrt{x} + 1) \).

#### Phân tích \( x - 2\sqrt{x} + 1 \):

Biểu thức \( x - 2\sqrt{x} + 1 \) có thể được viết lại dưới dạng một bình phương:

\[
x - 2\sqrt{x} + 1 = (\sqrt{x} - 1)^2
\]

Vì:

\[
(\sqrt{x} - 1)^2 = (\sqrt{x})^2 - 2 \cdot \sqrt{x} \cdot 1 + 1^2 = x - 2\sqrt{x} + 1
\]

### Bước 2: Thay thế và đơn giản hóa

Thay vào biểu thức \( M \):

\[
M = \sqrt{25x^2 \cdot (\sqrt{x} - 1)^2}
\]

Khi thực hiện phép nhân bên trong dấu căn, ta có:

\[
25x^2 \cdot (\sqrt{x} - 1)^2
\]

### Bước 3: Rút gọn

Dùng thuộc tính căn bậc hai \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \):

\[
M = \sqrt{25x^2 \cdot (\sqrt{x} - 1)^2} = \sqrt{25x^2} \cdot \sqrt{(\sqrt{x} - 1)^2}
\]

Ta biết rằng:

\[
\sqrt{25x^2} = 5x
\]

Và:

\[
\sqrt{(\sqrt{x} - 1)^2} = |\sqrt{x} - 1|
\]

### Bước 4: Xác định dấu của \( \sqrt{x} - 1 \)

Vì \( 0 < x < 1 \), \( \sqrt{x} \) là một số dương nhỏ hơn 1. Do đó:

\[
\sqrt{x} - 1 < 0
\]

Vậy:

\[
|\sqrt{x} - 1| = 1 - \sqrt{x}
\]

### Bước 5: Kết hợp các kết quả

Vậy biểu thức rút gọn là:

\[
M = 5x \cdot (1 - \sqrt{x})
\]

### Kết luận

Biểu thức rút gọn của \( M \) là:

\[
M = 5x (1 - \sqrt{x})
\]

Để rút gọn biểu thức \( M = \sqrt{25x^2 \cdot (x - 2\sqrt{x} + 1)} \), ta sẽ tiến hành theo các bước sau:

### Bước 1: Phân tích biểu thức bên trong căn
Biểu thức bên trong căn là \( 25x^2 \cdot (x - 2\sqrt{x} + 1) \).

Trước tiên, ta nhận thấy rằng biểu thức \( x - 2\sqrt{x} + 1 \) có thể được viết lại dưới dạng hiệu của một bình phương hoàn hảo.

Ta có:
\[
x - 2\sqrt{x} + 1 = (\sqrt{x} - 1)^2
\]

### Bước 2: Thay vào biểu thức
Thay vào biểu thức \( M \):
\[
M = \sqrt{25x^2 \cdot (\sqrt{x} - 1)^2}
\]

### Bước 3: Tính căn bậc hai
Ta có thể phân tích căn bậc hai bên trong:
\[
M = \sqrt{25} \cdot \sqrt{x^2} \cdot \sqrt{(\sqrt{x} - 1)^2}
\]

Tính từng phần:
\[
\sqrt{25} = 5, \quad \sqrt{x^2} = x \quad (\text{vì } x > 0)
\]

Và:
\[
\sqrt{(\sqrt{x} - 1)^2} = |\sqrt{x} - 1|
\]

### Bước 4: Xác định dấu của \( \sqrt{x} - 1 \) trong khoảng \( 0 < x < 1 \)
Khi \( 0 < x < 1 \), ta có \( \sqrt{x} < 1 \), từ đó:
\[
\sqrt{x} - 1 < 0 \Rightarrow |\sqrt{x} - 1| = 1 - \sqrt{x}
\]

### Bước 5: Kết hợp lại
Vậy biểu thức \( M \) trở thành:
\[
M = 5 \cdot x \cdot (1 - \sqrt{x}) = 5x(1 - \sqrt{x})
\]

### Kết quả
Vậy, biểu thức đã rút gọn là:
\[
M = 5x(1 - \sqrt{x}) \quad \text{(với } 0 < x < 1\text{)}
\]