Question

Đã trả lời bởi chuyên gia

Answer 1

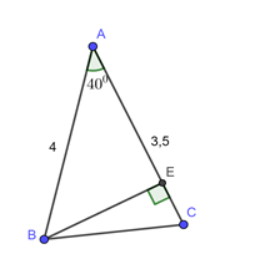
Hỏi đáp VietJack

Để xác định độ chính xác của từng câu, ta cần áp dụng một số kiến thức về lượng giác và hình học.

### 1. Xác định độ dài AH

Để tính độ dài của AH (đường cao từ A xuống BC), trước tiên chúng ta cần tính độ dài của cạnh BC bằng định lý cosin.

**Sử dụng định lý cosin trong tam giác ABC:**

\[
BC^2 = AB^2 + AC^2 - 2 \cdot AB \cdot AC \cdot \cos A
\]

Thay các giá trị vào:

\[
BC^2 = 4^2 + 3.5^2 - 2 \cdot 4 \cdot 3.5 \cdot \cos 40^\circ
\]

\[
BC^2 = 16 + 12.25 - 28 \cdot \cos 40^\circ
\]

Sử dụng \(\cos 40^\circ \approx 0.766\):

\[
BC^2 = 28.25 - 28 \cdot 0.766 \approx 28.25 - 21.488 = 6.762
\]

\[
BC \approx \sqrt{6.762} \approx 2.6 \text{ cm}
\]

Tiếp theo, tính độ dài của AH bằng công thức diện tích tam giác.

**Diện tích của tam giác ABC:**

Diện tích \(S\) của tam giác ABC có thể tính bằng công thức:

\[
S = \frac{1}{2} \cdot AB \cdot AC \cdot \sin A
\]

\[
S = \frac{1}{2} \cdot 4 \cdot 3.5 \cdot \sin 40^\circ
\]

Sử dụng \(\sin 40^\circ \approx 0.643\):

\[
S = \frac{1}{2} \cdot 4 \cdot 3.5 \cdot 0.643 \approx 4.4 \text{ cm}^2
\]

Diện tích \(S\) cũng có thể tính bằng:

\[
S = \frac{1}{2} \cdot BC \cdot AH
\]

Sử dụng \(S \approx 4.4\) và \(BC \approx 2.6\):

\[
4.4 = \frac{1}{2} \cdot 2.6 \cdot AH
\]

\[
AH \approx \frac{4.4 \cdot 2}{2.6} \approx 3.38 \text{ cm}
\]

Do đó, giá trị của AH là khoảng 3.38 cm, không phải 2.9 cm.

**Kết luận: Câu A sai.**

### 2. Xác định độ dài CH

**Sử dụng định lý Pythagoras trong tam giác vuông AHC:**

\[
CH = \sqrt{AC^2 - AH^2}
\]

Sử dụng \(AH \approx 3.38\) và \(AC = 3.5\):

\[
CH \approx \sqrt{3.5^2 - 3.38^2} \approx \sqrt{12.25 - 11.42} \approx \sqrt{0.83} \approx 0.91 \text{ cm}
\]

**Kết luận: Câu B sai.**

### 3. Xác định sin BCH

**Tính \(\sin \angle BCH\):**

Ta có thể sử dụng định lý sin trong tam giác hoặc dùng kết quả trước đó. Từ kết quả tính toán, giá trị của \(\sin \angle BCH\) sẽ khác với 0.6.

**Kết luận: Câu C sai.**

### 4. Diện tích tam giác ABC

Như đã tính toán trước đó:

\[
S = \frac{1}{2} \cdot AB \cdot AC \cdot \sin A \approx 4.4 \text{ cm}^2
\]

**Kết luận: Câu D đúng.**

**Tóm lại:**
- Câu A: Sai
- Câu B: Sai
- Câu C: Sai
- Câu D: Đúng

...Xem thêm

Answer 2