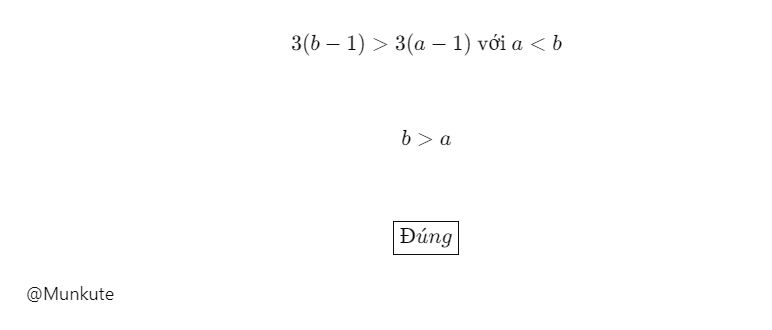Quảng cáo
2 câu trả lời 968
Để chứng minh bất đẳng thức \(3(b - 1) > 3(a - 1)\) với điều kiện \(a < b\), chúng ta thực hiện các bước sau:
1. **Bắt đầu với điều kiện \(a < b\):**
\(a < b\)
2. **Nhân cả hai vế của bất đẳng thức với 3:**
Vì \(3\) là một số dương, nên nhân vào bất đẳng thức không làm thay đổi chiều của dấu bất đẳng thức. Do đó:
\[
3a < 3b
\]
3. **Trừ \(3\) từ cả hai vế của bất đẳng thức:**
Ta trừ \(3\) từ cả hai vế của bất đẳng thức:
\[
3a - 3 < 3b - 3
\]
4. **Viết lại bất đẳng thức:**
Ta có thể viết lại bất đẳng thức trên dưới dạng:
\[
3(a - 1) < 3(b - 1)
\]
5. **Đảo chiều bất đẳng thức:**
Ta đổi chiều bất đẳng thức để khớp với bất đẳng thức cần chứng minh:
\[
3(b - 1) > 3(a - 1)
\]
Vậy, ta đã chứng minh rằng nếu \(a < b\), thì \(3(b - 1) > 3(a - 1)\).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211