Quảng cáo
3 câu trả lời 1334
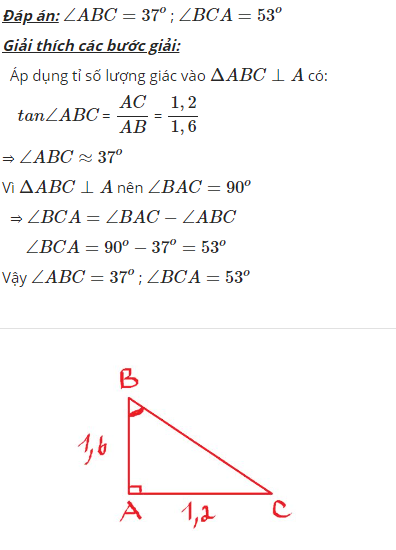
áp dụng định lí pythagore vào tam ABC ( góc A = 90 độ) ta có:
BC2= AB2+ AC2 = 1,6 + 1,2 = 2,8
suy ra BC= = 1,7
Các tỉ số lượng giác của góc B là :
sin B = cos B = tanB = cotB =
Các tỉ số lượng giác của góc C là:
sinC= cosC = tanC = cotC =
Trong tam giác vuông ABC tại A, chúng ta có các cạnh như sau:
- \( AB = 1.6 \, \text{cm} \) (cạnh đối diện với góc C)
- \( AC = 1.2 \, \text{cm} \) (cạnh đối diện với góc B)
- Cạnh huyền \( BC \) sẽ được tính bằng định lý Pythagore.
### Bước 1: Tính độ dài cạnh huyền BC
Theo định lý Pythagore:
\[
BC^2 = AB^2 + AC^2
\]
\[
BC^2 = (1.6)^2 + (1.2)^2 = 2.56 + 1.44 = 4
\]
\[
BC = \sqrt{4} = 2 \, \text{cm}
\]
### Bước 2: Tính tỷ số lượng giác của góc B
- **Sin B** (sin của góc B):
\[
\sin B = \frac{AC}{BC} = \frac{1.2}{2} = 0.6
\]
- **Cos B** (cos của góc B):
\[
\cos B = \frac{AB}{BC} = \frac{1.6}{2} = 0.8
\]
- **Tan B** (tan của góc B):
\[
\tan B = \frac{AC}{AB} = \frac{1.2}{1.6} = 0.75
\]
### Bước 3: Tính tỷ số lượng giác của góc C
Trong tam giác vuông, có mối liên hệ giữa các góc B và C:
\[
\sin C = \cos B, \quad \cos C = \sin B, \quad \tan C = \frac{1}{\tan B}
\]
- **Sin C**:
\[
\sin C = \cos B = 0.8
\]
- **Cos C**:
\[
\cos C = \sin B = 0.6
\]
- **Tan C**:
\[
\tan C = \frac{1}{\tan B} = \frac{1}{0.75} = \frac{4}{3} \approx 1.3333
\]
### Kết luận
- Tỷ số lượng giác của góc B:
- \(\sin B = 0.6\)
- \(\cos B = 0.8\)
- \(\tan B = 0.75\)
- Tỷ số lượng giác của góc C:
- \(\sin C = 0.8\)
- \(\cos C = 0.6\)
- \(\tan C \approx 1.3333\)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387