Question

Đã trả lời bởi chuyên gia

Answer 1

đáp án nha

Hỏi đáp VietJack

Answer 2

Để tính các đoạn thẳng \( AB, BH, AC, BC \) trong tam giác \( ABC \) với thông tin như sau:

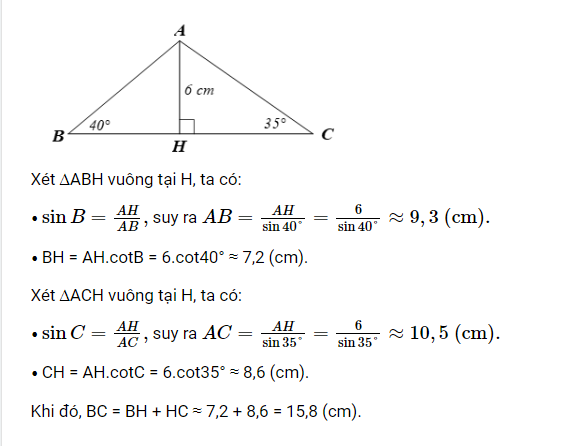
- Đường cao \( AH = 6 \) cm
- Góc \( B = 40^\circ \)
- Góc \( C = 35^\circ \)

### 1. Tính góc A

Góc \( A \) có thể được tính bằng cách sử dụng tổng các góc trong tam giác:

\[
A = 180^\circ - B - C = 180^\circ - 40^\circ - 35^\circ = 105^\circ
\]

### 2. Tính độ dài các cạnh của tam giác

Do có độ cao \( AH \) từ \( A \) xuống cạnh \( BC \), nên ta có thể áp dụng công thức liên quan đến chiều cao và các cạnh trong tam giác.

#### a. Tính cạnh \( BC \)

Ta sẽ sử dụng định lý sin và công thức cho đường cao. Đầu tiên, áp dụng công thức:

\[
AH = \frac{a \cdot \sin A}{a}
\]

Trong đó \( a = BC \).

Từ định lý sin, ta có:

\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
\]

Vì vậy:

\[
\frac{BC}{\sin A} = \frac{AH}{\sin C}
\]

Thay vào đó:

\[
BC = AH \cdot \frac{\sin A}{\sin C}
\]

#### b. Tính góc cho từng cạnh

\[
\sin A = \sin 105^\circ \approx 0.9659
\]

\[
\sin C = \sin 35^\circ \approx 0.5736
\]

Áp dụng để tính cạnh \( BC \):

\[
BC = 6 \cdot \frac{0.9659}{0.5736} \approx 6 \cdot 1.6841 \approx 10.10 \text{ cm}
\]

### 3. Tính các cạnh còn lại

#### c. Tính cạnh \( AC \)

Sử dụng tương tự cho \( AC \):

\[
AC = AH \cdot \frac{\sin B}{\sin C}
\]

\[
AC = 6 \cdot \frac{\sin 40^\circ}{\sin 35^\circ}
\]

Tính toán cho \( \sin 40^\circ \):

\[
\sin 40^\circ \approx 0.6428
\]

Áp dụng vào công thức:

\[
AC = 6 \cdot \frac{0.6428}{0.5736} \approx 6 \cdot 1.120 \approx 6.72 \text{ cm}
\]

#### d. Tính cạnh \( AB \)

Tương tự:

\[
AB = AH \cdot \frac{\sin C}{\sin A}
\]

Thay vào:

\[
AB = 6 \cdot \frac{\sin 35^\circ}{\sin 105^\circ}
\]

\[
AB = 6 \cdot \frac{0.5736}{0.9659} \approx 6 \cdot 0.5932 \approx 3.56 \text{ cm}
\]

### 4. Tính đoạn \( BH \)

Biết rằng \( H \) là chân đường cao từ \( A \), để tính \( BH \) ta có thể sử dụng góc \( B \) và chiều cao \( AH \).

Sử dụng định lý sin:

\[
BH = AH \cdot \tan B = 6 \cdot \tan 40^\circ
\]

Tính \( \tan 40^\circ \):

\[
\tan 40^\circ \approx 0.8391
\]

Vậy:

\[
BH = 6 \cdot 0.8391 \approx 5.04 \text{ cm}
\]

### Tổng kết

Sau khi tính toán, ta có các đoạn thẳng như sau:

- \( AB \approx 3.56 \text{ cm} \)
- \( AC \approx 6.72 \text{ cm} \)
- \( BC \approx 10.10 \text{ cm} \)
- \( BH \approx 5.04 \text{ cm} \)

Nếu có thắc mắc hay yêu cầu nào thêm, hãy cho tôi biết nhé!

...Xem thêm

Answer 3