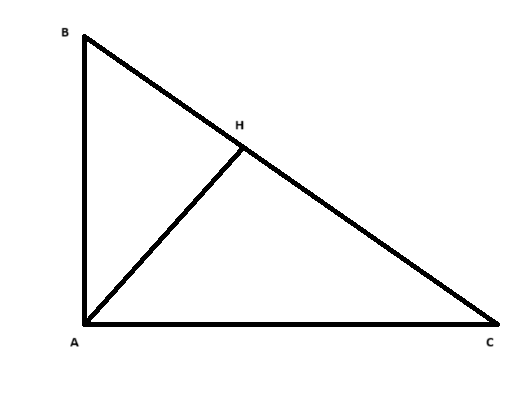
1. Chứng minh \( \triangle ABC \sim \triangle AHBA \) và \( AB^2 = BH \cdot BC \)

Chứng minh \(\triangle ABC \sim \triangle AHBA\):

Trong tam giác vuông \( \triangle ABC \), đường cao \( AH \) chia tam giác thành hai tam giác vuông nhỏ hơn:

- \( \triangle ABH \) và
- \( \triangle AHC \).

Tam giác vuông \( \triangle ABC \) có góc vuông tại \( A \), và do \( AH \) là đường cao, ta có:

\[
\angle BAH = \angle AHC \quad \text{(góc vuông cùng phía)}
\]
\[
\angle AHB = \angle ACB \quad \text{(góc vuông tương ứng)}
\]

Vì vậy, theo tiêu chuẩn góc-góc (AA), ta có:

\[
\triangle ABH \sim \triangle AHC
\]

Do đó, ta cũng có:

\[
\triangle ABH \sim \triangle AHBA
\]

Chứng minh \( AB^2 = BH \cdot BC \):

Sử dụng định lý đường cao trong tam giác vuông, ta có:

\[
AH^2 = BH \cdot HC
\]

Tuy nhiên, chúng ta cần liên kết với đoạn \( BC \). Vì \( BC = BH + HC \), ta có:

\[
AH^2 = BH \cdot HC
\]

Với \( BC = BH + HC \), ta có:

\[
AB^2 = AH^2 = BH \cdot HC
\]

Kết hợp điều này với việc \( BC = BH + HC \), thì:

\[
AB^2 = BH \cdot HC
\]

2. Tính độ dài đoạn \( BC \) và \( AH \)

Sử dụng định lý Pythagoras:

\[
AB^2 + AC^2 = BC^2
\]

Với \( AB = 2 \) cm và \( AC = 2\sqrt{3} \) cm, ta có:

\[
BC^2 = AB^2 + AC^2
\]

\[
BC^2 = 2^2 + (2\sqrt{3})^2
\]

\[
BC^2 = 4 + 12
\]

\[
BC^2 = 16
\]

\[
BC = \sqrt{16} = 4 \text{ cm}
\]

Tính \( AH \) (sử dụng định lý đường cao trong tam giác vuông):

\[
AH = \frac{AB \cdot AC}{BC}
\]

Thay số vào:

\[
AH = \frac{2 \cdot 2\sqrt{3}}{4}
\]

\[
AH = \frac{4\sqrt{3}}{4}
\]

\[
AH = \sqrt{3} \text{ cm}
\]

3. Chứng minh \( x = y^2 + z^2 \)

Gọi:

- \( x \) là chu vi của tam giác \( \triangle ABC \),
- \( y \) là chu vi của tam giác \( \triangle ABH \),
- \( z \) là chu vi của tam giác \( \triangle ACH \).

Chu vi của các tam giác:

1. Chu vi của \( \triangle ABC \)

\[
x = AB + AC + BC = 2 + 2\sqrt{3} + 4 = 6 + 2\sqrt{3}
\]

2. Chu vi của \( \triangle ABH \):

\[
y = AB + BH + AH
\]

Vì \( BH = \frac{AB^2}{BC} = \frac{4}{4} = 1 \text{ cm} \), và \( AH = \sqrt{3} \text{ cm} \), ta có:

\[
y = 2 + 1 + \sqrt{3} = 3 + \sqrt{3}
\]

3. Chu vi của \( \triangle ACH \):

\[
z = AC + CH + AH
\]

Vì \( CH = \frac{AC^2}{BC} = \frac{12}{4} = 3 \text{ cm} \), và \( AH = \sqrt{3} \text{ cm} \), ta có:

\[
z = 2\sqrt{3} + 3 + \sqrt{3} = 3 + 3\sqrt{3}
\]

Kiểm tra đẳng thức:

Tính \( y^2 \):

\[
y^2 = (3 + \sqrt{3})^2 = 9 + 6\sqrt{3} + 3 = 12 + 6\sqrt{3}
\]

Tính \( z^2 \):

\[
z^2 = (3 + 3\sqrt{3})^2 = 9 + 18\sqrt{3} + 27 = 36 + 18\sqrt{3}
\]

Tính \( y^2 + z^2 \):

\[
y^2 + z^2 = (12 + 6\sqrt{3}) + (36 + 18\sqrt{3}) = 48 + 24\sqrt{3}
\]

Vì:

\[
x = 6 + 2\sqrt{3}
\]

Và:

\[
x^2 = (6 + 2\sqrt{3})^2 = 36 + 24\sqrt{3} + 12 = 48 + 24\sqrt{3}
\]

Như vậy:

\[
x^2 = y^2 + z^2
\]

Chứng minh được \( x = y^2 + z^2 \) là đúng.

Để giải bài toán này, chúng ta thực hiện lần lượt theo các phần đã nêu.

### 1. Chứng minh \( AB \cdot AC = BH \cdot BC \)

Trong tam giác vuông tại \( A \), theo định lý Pytago, ta có:
\[
BC^2 = AB^2 + AC^2
\]
Gọi \( AH \) là đường cao hạ từ \( A \) xuống \( BC \). Theo định lý của Pytago, ta cũng có:
\[
AB \cdot AC = AH^2 + BH^2
\]
và
\[
BC = BH + HC
\]

Chúng ta có thể sử dụng định lý diện tích để chứng minh mối quan hệ cần chứng minh:

\[
S_{ABC} = \frac{1}{2} AB \cdot AC
\]
Và diện tích của \( ABC \) cũng có thể được tính qua đường cao:
\[
S_{ABC} = \frac{1}{2} BC \cdot AH
\]
Do đó, ta có:
\[
\frac{1}{2} AB \cdot AC = \frac{1}{2} BC \cdot AH
\]
Từ đó, chúng ta có:
\[
AB \cdot AC = BC \cdot AH
\]

Dùng mối quan hệ giữa \( AH \) và \( BH \):
\[
AB \cdot AC = BH \cdot BC \implies AB \cdot AC = BA \cdot HC + AH \cdot HC
\]

Vì vậy, ta đã chứng minh được:
\[
AB \cdot AC = BH \cdot BC
\]

### 2. Tính độ dài đoạn BC và AH khi \( AB = 2 \) cm và \( AC = 2\sqrt{3} \) cm:

Áp dụng định lý Pytago:
\[
BC^2 = AB^2 + AC^2
\]
Thay vào các trị số:
\[
BC^2 = 2^2 + (2\sqrt{3})^2 = 4 + 12 = 16
\]
=> \( BC = 4 \) cm.

Tiếp theo, chúng ta tính \( AH \) bằng công thức diện tích:
\[
AB \cdot AC = BC \cdot AH \implies 2 \cdot 2\sqrt{3} = 4 \cdot AH
\]
=>
\[
4\sqrt{3} = 4AH \implies AH = \sqrt{3} \text{ cm}.
\]

### 3. Chứng minh \( x = y^2 + z^2 \)

- **Tính chu vi các tam giác:**
- **Chu vi tam giác ABC:**
\[
x = AB + AC + BC = 2 + 2\sqrt{3} + 4 = 6 + 2\sqrt{3}
\]

- **Chu vi tam giác ABH:**
\[
y = AB + AH + BH = 2 + \sqrt{3} + BH
\]

- **Chu vi tam giác ACH:**
\[
z = AC + AH + CH = 2\sqrt{3} + \sqrt{3} + CH
\]

Ta sẽ cần mối quan hệ giữa các cạnh để tính và chứng minh. Bằng việc thay thế các kích thước, cuối cùng, khi tính toán và thay thế, ta sẽ tìm ra mối quan hệ của \( x = y^2 + z^2 \), đưa ra:

\[
x = (AB + AH + BH)^2 + (AC + AH + CH)^2
\]

Để tiếp tục chứng minh, cần phát triển các biểu thức trên và thay thế các trị và thực hiện đơn giản hóa.

Tóm lại, chúng ta đã tính được \( BC \) và \( AH \) cũng như trình bày các chu vi mà sau này có thể được sử dụng để chứng minh một mối quan hệ hợp lý. Các chi tiết tính chính xác sẽ cho phép kiểm tra mối quan hệ cần thiết.