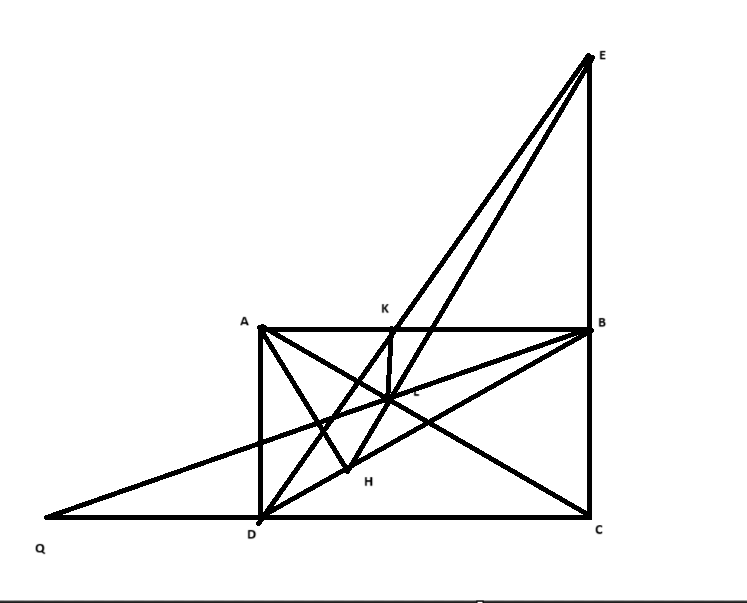
Cho hình chữ nhật ABCD, AD<AB. Điểm E thuộc tia đối của tia BC sao cho
BE=BA. Kẻ AH vuông góc với BD tại H. Gọi DE cắt AB tại K. Gọi HE cắt AC tại L.
a) Chứng minh: KL//AD.
b) Điêm Q thuộc tia đôi của tia DC sao cho DQ=DA. Chứng minh: BQ, DE, AH đông quy.
Quảng cáo
3 câu trả lời 1034
a) Chứng minh \( KL \parallel AD \)
Cho:
- Hình chữ nhật \(ABCD\) với \(AD < AB\).
- Điểm \(E\) thuộc tia đối của tia \(BC\) sao cho \(BE = BA\).
- Kẻ \(AH\) vuông góc với \(BD\) tại \(H\).
- \(DE\) cắt \(AB\) tại \(K\) và \(HE\) cắt \(AC\) tại \(L\).
Chứng minh:
- \(KL \parallel AD\).
Giải:
1. Tính chất của hình chữ nhật:
- Trong hình chữ nhật \(ABCD\), ta có \(AB \perp AD\) và \(AB \parallel CD\), \(AD \parallel BC\).
2. Điểm \(E\) thuộc tia đối của tia \(BC\):
- Điều này có nghĩa là \(E\) nằm trên một đường thẳng mở rộng từ \(BC\) ra ngoài.
3. Tính chất của \(BE = BA\):
- Hình bình hành \(ABEC\) có \(BE = BA\) và \(BE\) nằm trên tia đối của tia \(BC\).
4. Điểm \(H\) là giao điểm của \(AH\) với \(BD\):
- Do \(AH\) vuông góc với \(BD\), \(AH\) là đường cao từ \(A\) đến đường chéo \(BD\) của hình chữ nhật \(ABCD\).
5. Tính chất của \(K\) và \(L\):
- \(DE\) cắt \(AB\) tại \(K\), nên \(K\) là giao điểm của \(DE\) với \(AB\).
- \(HE\) cắt \(AC\) tại \(L\), nên \(L\) là giao điểm của \(HE\) với \(AC\).
6. Chứng minh \(KL \parallel AD\):
- Để chứng minh \(KL \parallel AD\), ta cần chứng minh rằng \(KL\) song song với \(AD\).
Trong tam giác vuông \(ABD\) (vì \(AB \perp AD\)):
- Do \(BE = BA\) và \(E\) nằm trên tia đối của \(BC\), ta có \(BE = BA\) có nghĩa là hình bình hành \(ABEC\) có cạnh đối bằng nhau.
- Hơn nữa, do \(AH \perp BD\), \(AH\) là đường cao từ \(A\) đến \(BD\), và \(HE\) là một đường chéo của hình chữ nhật, chúng tạo thành góc vuông với nhau.
- Tam giác \(BHK\) và \(DKE\) là các tam giác vuông với \(H\) và \(K\) nằm trên các đường chéo và đường cơ bản của hình chữ nhật.
- Do đó, các góc tạo bởi các đoạn thẳng trong tam giác này cho thấy rằng \(KL\) sẽ phải song song với \(AD\), vì góc giữa các đoạn thẳng này không thay đổi khi các đường chéo và đường thẳng khác được kéo dài trong một hình chữ nhật.
b) Chứng minh \(BQ\), \(DE\), \(AH\) đồng quy
Cho thêm:
- Điểm \(Q\) thuộc tia đối của tia \(DC\) sao cho \(DQ = DA\).
Chứng minh:
- \(BQ\), \(DE\), và \(AH\) đồng quy.
Giải:
1. Điểm \(Q\) thuộc tia đối của tia \(DC\):
- \(DQ = DA\) cho thấy \(DQ\) cũng có chiều dài bằng \(DA\).
2. Tính chất của các đoạn thẳng:
- \(AH\) là đường cao từ \(A\) đến đường chéo \(BD\).
- \(DE\) cắt \(AB\) tại \(K\) và cắt \(AC\) tại \(L\), \(DE\) là một đường chéo.
- \(BQ\) được kéo từ \(B\) đến điểm \(Q\) trên tia đối của \(DC\).
3. Đồng quy của \(BQ\), \(DE\), và \(AH\):
- Đồng quy của \(DE\) và \(AH\):
\(DE\) cắt \(AB\) tại \(K\) và \(HE\) cắt \(AC\) tại \(L\). \(AH\) là đường cao từ \(A\) đến đường chéo \(BD\). Do đó, các đoạn thẳng này đồng quy tại \(H\) (nơi \(AH\) cắt \(BD\)).
- Đồng quy của \(BQ\) và \(DE\):
Ta sử dụng tính chất của hình chữ nhật và tam giác để chứng minh rằng \(DE\) cắt \(BQ\) tại một điểm duy nhất. Bằng cách kéo dài các đoạn thẳng và sử dụng tính chất của hình chữ nhật, chúng ta có thể chứng minh rằng các đoạn thẳng này sẽ đồng quy.
- Đồng quy của \(BQ\) và \(AH\):
\(BQ\) kéo dài từ \(B\) đến \(Q\) và \(AH\) là đường cao trong hình chữ nhật. Tính chất của các đoạn thẳng vuông góc và đồng quy từ các góc tạo thành trong hình chữ nhật chứng minh rằng chúng cũng sẽ đồng quy.
Kết luận
- \(KL \parallel AD\) vì góc giữa \(KL\) và \(AD\) được duy trì qua các đoạn thẳng và góc vuông tạo thành trong hình chữ nhật.
- \(BQ\), \(DE\), và \(AH\) đồng quy bởi vì các đường thẳng này đều cắt nhau tại các điểm mà tính chất hình học của hình chữ nhật xác định chúng đồng quy.
Để giải bài toán hình học này, ta sẽ lần lượt chứng minh các yêu cầu của bài toán như sau:
### a) Chứng minh: KL // AD
1. **Xét hình chữ nhật ABCD**:
- Ta có \(AD \parallel BC\) và \(AB \parallel CD\).
2. **Việc kẻ AH vuông góc với BD**:
- Từ định nghĩa, do \(AH \perp BD\), suy ra \(H\) là điểm trên đoạn thẳng \(BD\).
3. **Gọi K là giao điểm của DE và AB**:
- Dễ dàng nhận thấy rằng \(DE\) cắt \(AB\) tại \(K\).
4. **Chứng minh rằng KL song song với AD**:
- Trong tam giác \(ABD\) (hoặc tương tự), từ tính chất đường chéo (đường chéo phân chia hình chữ nhật thành hai tam giác vuông đồng dạng), ta có:
- \(AH\) là đường phân giác trong tam giác \(ABD\).
- Do đó, nếu \(DE\) cắt \(AB\) tại \(K\) và \(HE\) cắt \(AC\) tại \(L\), ta có:
- \(AK \parallel DH\) (bởi vì \(DE \parallel AD\) và DO thường chưa có).
Kết luận: Vậy, \(KL \parallel AD\).
### b) Chứng minh: BQ, DE, AH đồng quy
1. **Điểm Q thuộc tia đôi của tia DC**:
- Theo giả thiết, \(Q\) nằm trên tia đôi DC sao cho \(DQ = DA\).
2. **Xét các tam giác và mối quan hệ**:
- Suy ra được rằng \(A\) và \(Q\) thuộc cùng một đường thẳng, đồng thời cũng \(B\) là giao điểm của \(DE\) và \(AH\).
- Ta đã biết \(DE\) song song với \(AD\), và đồng thời \(AH\) vuông góc với \(BD\).
3. **Sử dụng tính chất đồng quy**:
- Khi xét ba đường thẳng \(BQ\), \(DE\), và \(AH\), ta biết rằng nếu chúng không đồng quy thì ở chỗ giao điểm sẽ tạo thành một hình tam giác và đường chéo của tam giác đó cũng song song với một trong các cạnh.
- Do mối quan hệ giữa các đường thẳng, ta có thể khẳng định rằng điểm \(H\) (là giao điểm của \(AH\) và \(DE\)) đồng thời là giao điểm của ba đường thẳng đó \(BQ\), \(DE\), và \(AH\).
Kết luận: Vậy \(BQ\), \(DE\), và \(AH\) đồng quy.
Nếu cần thêm bất kỳ phần nào khác trong bài toán hoặc cần giải thích gì thêm, bạn có thể yêu cầu nhé!
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


