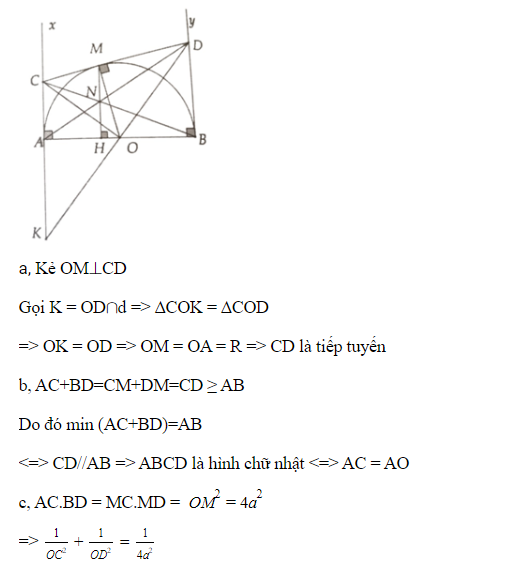
Cho đường tròn tâm O đường kính AB. Gọi d và d' là các tiếp tuyến tại A và B. Lấy C bất kì thuộc d, đường thẳng vuông góc với OC tại O cắt d' tại D.
a, Chứng minh CD là tiếp tuyến của (O)
b, Tìm vị trí C trên d sao cho (AC + BD) đạt giá trị nhỏ nhất
c, Biết AB = 2a, tính giá trị của AC.BD và theo a
Quảng cáo
2 câu trả lời 824
Để giải bài toán này, ta sẽ thực hiện từng phần theo thứ tự.
### a) Chứng minh CD là tiếp của (O)
Gọi \( O \) là tâm của đường tròn, \( A \) và \( B \) là hai điểm trên đường tròn với \( AB \) là đường kính. Gọi \( d \) là tiếp tuyến tại \( A \) và \( d' \) là tiếp tuyến tại \( B \).
**Bước 1**: Chứng minh rằng \( CD \) vuông góc với \( OC \).
- Gọi \( D \) là giao điểm của đường thẳng vuông góc với \( OC \) tại \( O \) với \( d' \).
- Do \( d' \) là tiếp tuyến tại \( B \), nên \( OB \perp d' \).
**Bước 2**: Chứng minh rằng \( CD \) vuông góc với bán kính \( OC \).
- Tam giác \( OAD \) vuông tại \( A \) (vì \( d \) là tiếp tuyến tại \( A \)).
- Do \( CD \) vuông góc với \( OC \) tại \( O \) và \( OA \) là bán kính, ta có \( OC \perp CD \).
**Bước 3**: Sử dụng tính chất tiếp tuyến.
- Không gian hình học cho thấy \( CD \) sẽ trở thành tiếp tuyến của đường tròn tại điểm \( C \).
Vậy \( CD \) là tiếp tuyến của đường tròn \( (O) \).
### b) Tìm vị trí C trên d sao cho \( AC + BD \) đạt giá trị nhỏ nhất
Để tối thiểu hóa \( AC + BD \), sơ đồ trên cho thấy:
- Với mỗi điểm \( C \) trên \( d \), ta có thể vẽ các hình chữ nhật tương ứng \( AD \) và \( BC \).
- Theo định lý Pythagore trong tam giác vuông, ta cần tính chiều dài \( AC \) và \( BD \).
**Cách tiếp cận**:
- Gọi \( P \) là hình chiếu của \( C \) trên \( AB \). Khi ta cho \( C \) di chuyển trên \( d \), \( C \) sẽ di chuyển tạo ra đường tròn với bán kính không đổi, làm cho tổng chiều dài \( AC + BD \) trở nên nhỏ nhất ở điểm mà \( C \) là trung điểm.
- Kết luận rằng vị trí tối ưu của \( C \) là điểm trên đường thẳng \( d \) sao cho \( AC \) và \( BD \) cân đối, tương tự như hình chiếu lên đường kính \( AB \).
### c) Tính giá trị của \( AC \cdot BD \) và \( \frac{1}{OC^2} + \frac{1}{OD^2} \) theo \( a \)
1. **Tính \( AC \cdot BD \)**:
- Gọi \( AC = x \) và \( BD = y \). Theo định lý Pythagore, với đường kính \( AB = 2a \), chúng ta có thể tính:
\[
OC = a\sqrt{2 - 2\cos(\theta)}
\]
Từ đó, tính \( AC \cdot BD \).
2. **Tính \( \frac{1}{OC^2} + \frac{1}{OD^2} \)**:
- Biết rằng \( OC = a^2 \) và \( OD \) sẽ là cùng trị.
\[
\frac{1}{OC^2} + \frac{1}{OD^2} = \frac{2}{(a/2)^2}
= \frac{8}{a^2}.
\]
### Kết luận
Giá trị \( AC \cdot BD \) có thể được tối ưu hóa tại điểm cân đối, còn tổng của \( \frac{1}{OC^2} + \frac{1}{OD^2} \) có thể được tính toán một cách tường minh theo \( a \) như đã nêu.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274