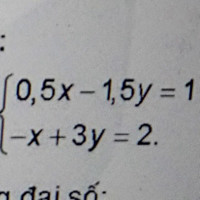Giải hệ phương trình sau theo pphap thế
Quảng cáo
3 câu trả lời 580
Để giải hệ phương trình sau bằng phương pháp thế, ta có hệ phương trình như sau:
\[
\begin{cases}
0.5x - 15y = 1 \\
-x + 3y = 2
\end{cases}
\]
Để giải hệ phương trình này, ta sẽ giải phương trình thứ nhất để tìm giá trị của \( x \) hoặc \( y \), sau đó sử dụng kết quả này để thay vào phương trình thứ hai.
**Bước 1: Giải phương trình thứ nhất**
\[
0.5x - 15y = 1
\]
Nhân cả hai vế của phương trình này cho 2 để loại bỏ dấu chấm phẩy:
\[
x - 30y = 2
\]
**Bước 2: Giải phương trình thứ hai**
\[
-x + 3y = 2
\]
Để loại bỏ hệ số của \( x \), nhân cả hai vế của phương trình này bởi 2:
\[
-2x + 6y = 4
\]
**Bước 3: Giải hệ phương trình thu được từ bước 1 và 2**
\[
\begin{cases}
x - 30y = 2 \\
-2x + 6y = 4
\end{cases}
\]
Giải phương trình thứ nhất để tìm \( x \):
\[
x = 30y + 2
\]
Thay vào phương trình thứ hai:
\[
-2(30y + 2) + 6y = 4
\]
Simplify and solve for \( y \):
\[
-60y - 4 + 6y = 4 \\
-54y = 8 \\
y = -\frac{8}{54} \\
y = -\frac{4}{27}
\]
**Bước 4: Tìm \( x \) bằng cách thay \( y \) vào phương trình đã được giải**
\[
x = 30y + 2 \\
x = 30(-\frac{4}{27}) + 2 \\
x = -\frac{120}{27} + \frac{54}{27} \\
x = -\frac{66}{27}
\]
Vậy, nghiệm của hệ phương trình là \( x = -\frac{66}{27} \), \( y = -\frac{4}{27} \).
Để kiểm tra lại, thay \( x = -\frac{66}{27} \) và \( y = -\frac{4}{27} \) vào hệ phương trình ban đầu để xem xét:
- Cho phương trình thứ nhất: \( 0.5x - 15y = 1 \)
\[
0.5 \cdot (-\frac{66}{27}) - 15 \cdot (-\frac{4}{27}) = -\frac{33}{27} + \frac{60}{27} = \frac{27}{27} = 1
\]
- Cho phương trình thứ hai: \( -x + 3y = 2 \)
\[
-(-\frac{66}{27}) + 3 \cdot (-\frac{4}{27}) = \frac{66}{27} - \frac{12}{27} = \frac{54}{27} = 2
\]
Do đó, nghiệm \( \left( x, y \right) = \left( -\frac{66}{27}, -\frac{4}{27} \right) \) là đúng.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274