Quảng cáo
2 câu trả lời 383
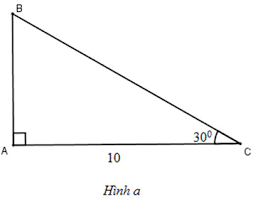
Để tính các tỉ số lượng giác của góc B trong tam giác vuông ABC, ta cần xác định độ dài của các cạnh của tam giác.
\Bước 1: Tìm độ dài của các cạnh\
Tam giác ABC vuông tại A, có \( BC = 8 \) cm và \( \sin C = 0,5 \).
Từ \(\sin C = 0,5\), ta có:
\[ \sin C = \frac{đối}{huyền} \]
Trong tam giác vuông, cạnh đối diện góc C là \( AB \) và cạnh huyền là \( BC \). Do đó:
\[ \sin C = \frac{AB}{BC} = \frac{AB}{8} \]
Vì \(\sin C = 0,5\), ta có:
\[ 0,5 = \frac{AB}{8} \]
\[ AB = 0,5 \times 8 = 4 \text{ cm} \]
Bước 2: Tìm độ dài cạnh AC
Sử dụng định lý Pythagore trong tam giác vuông ABC:
\[ BC^2 = AB^2 + AC^2 \]
\[ 8^2 = 4^2 + AC^2 \]
\[ 64 = 16 + AC^2 \]
\[ AC^2 = 48 \]
\[ AC = \sqrt{48} = 4\sqrt{3} \text{ cm} \]
Bước 3: Tính các tỉ số lượng giác của góc B
Các tỉ số lượng giác của góc B bao gồm \(\sin B\), \(\cos B\), và \(\tan B\).
1. \(\sin B\):
\[ \sin B = \frac{AC}{BC} = \frac{4\sqrt{3}}{8} = \frac{\sqrt{3}}{2} \]
2. \(\cos B\):
\[ \cos B = \frac{AB}{BC} = \frac{4}{8} = 0,5 \]
3. \(\tan B\):
\[ \tan B = \frac{AC}{AB} = \frac{4\sqrt{3}}{4} = \sqrt{3} \]
Do đó, các tỉ số lượng giác của góc B là:
\[ \sin B = \frac{\sqrt{3}}{2} \]
\[ \cos B = 0,5 \]
\[ \tan B = \sqrt{3} \]
Để tính tỉ số lượng giác của góc B trong tam giác ABC, ta cần xác định giá trị của các cạnh và góc trong tam giác.
Vì tam giác ABC vuông tại A và sin(C) = 0.5, ta có: sin(C) = BC/AC 0.5 = 8/AC AC = 16 cm
Áp dụng định lý Pythagore trong tam giác vuông ABC: AB^2 + AC^2 = BC^2 AB^2 + 16^2 = 8^2 AB^2 + 256 = 64 AB^2 = 64 - 256 AB^2 = -192 AB = √(-192) (không tồn tại số thực)
Do đó, không thể tính được tỉ số lượng giác của góc B trong trường hợp này vì tam giác ABC không tồn tại trong không gian Euclid với các thông số đã cho.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


