Quảng cáo
2 câu trả lời 1790
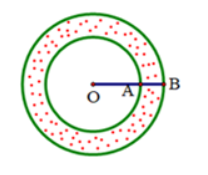
Để giải quyết bài toán này, ta cần sử dụng kiến thức về diện tích hình tròn và hình vành khăn.
Gọi \( R \) là bán kính của vòng ngoài của hình vành khăn. Diện tích hình vành khăn là hiệu của diện tích hai hình tròn có bán kính lần lượt là \( R \) và \( r \) (với \( r = 4 \, \text{m} \)).
Diện tích của vườn hoa (hình tròn nhỏ) là:
\[ S_{\text{hoa}} = \pi r^2 = \pi \times 4^2 = 16\pi \]
Diện tích của lối đi (hình vành khăn) là:
\[ S_{\text{đi}} = \pi R^2 - \pi r^2 \]
Theo đề bài, diện tích lối đi bằng 2 lần diện tích vườn hoa:
\[ S_{\text{đi}} = 2 \times S_{\text{hoa}} \]
\[ \pi R^2 - \pi r^2 = 2 \times 16\pi \]
\[ \pi R^2 - \pi \times 4^2 = 32\pi \]
\[ \pi R^2 - 16\pi = 32\pi \]
\[ \pi R^2 = 48\pi \]
\[ R^2 = 48 \]
\[ R = \sqrt{48} = 4\sqrt{3} \]
Khoảng cách giữa 2 điểm A và B là:
\[ AB = R = 4\sqrt{3} \]
Vậy khoảng cách giữa hai điểm A và B là \( 4\sqrt{3} \) mét.
Để giải bài toán này, ta cần tìm khoảng cách giữa hai điểm A và B trên đường kính của hình tròn.
Gọi B là điểm trên đường kính của hình tròn sao cho AB là khoảng cách giữa hai điểm A và B.
Diện tích của vườn hoa hình tròn là:
S_vuon = π * r^2 = π * 4^2 = 16π m^2
Diện tích của lối đi xung quanh hình vành khăn là:
S_loi_di = 2 * S_vuon = 2 * 16π = 32π m^2
Gọi x là bán kính của hình vành khăn, ta có:
Diện tích hình vành khăn = π * (R^2 - r^2) = 32π
=> π * (R^2 - 16) = 32π
=> R^2 - 16 = 32
=> R^2 = 48
=> R = √48 = 4√3 m
Vậy, khoảng cách giữa hai điểm A và B là bán kính hình vành khăn, tức là AB = R = 4√3 m.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


