7) Cho hai hàm số: y = x² có đồ thị là (P) và hàm số y = mx-5 có đồ thị là
đường thẳng (d).
a) Vẽ đồ thị hàm số (P)
b) Xác định hệ số m biết rằng đường thẳng (d) đi qua A(-1:0). c) Tìm m để đường thẳng (d) có đúng một điểm chung với (P).
8) Giải bài toán sau bằng cách lập phương trình
Quảng cáo
2 câu trả lời 197
### Bài 7
#### a) Vẽ đồ thị hàm số \( y = \frac{1}{2} x^2 \)
Đồ thị của hàm số \( y = \frac{1}{2} x^2 \) là một parabol có đỉnh tại gốc tọa độ (0,0) và mở lên trên. Một số điểm để vẽ đồ thị bao gồm:
- Khi \( x = -2 \), \( y = \frac{1}{2} (-2)^2 = 2 \)
- Khi \( x = -1 \), \( y = \frac{1}{2} (-1)^2 = \frac{1}{2} \)
- Khi \( x = 0 \), \( y = 0 \)
- Khi \( x = 1 \), \( y = \frac{1}{2} (1)^2 = \frac{1}{2} \)
- Khi \( x = 2 \), \( y = \frac{1}{2} (2)^2 = 2 \)
Sử dụng các điểm này, chúng ta có thể vẽ đồ thị của hàm số \( y = \frac{1}{2} x^2 \).
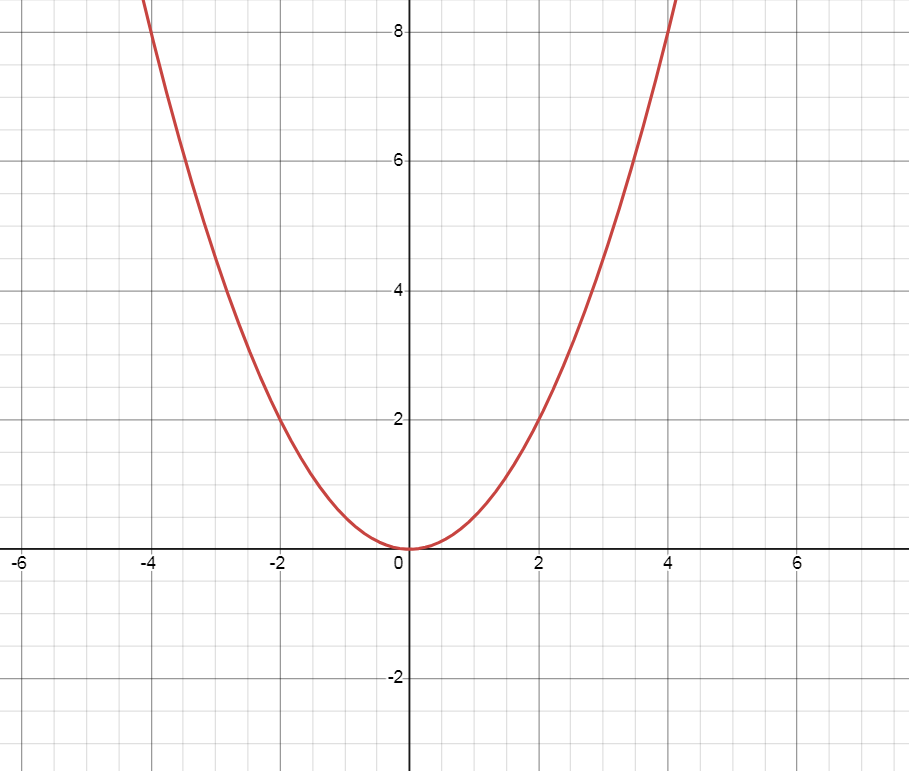
#### b) Xác định hệ số m biết rằng đường thẳng \( y = mx - 5 \) đi qua điểm \( A(-1, 0) \)
Điểm \( A(-1, 0) \) nằm trên đường thẳng \( y = mx - 5 \). Thay \( x = -1 \) và \( y = 0 \) vào phương trình của đường thẳng để tìm \( m \):
\[ 0 = m(-1) - 5 \]
\[ 0 = -m - 5 \]
\[ m = -5 \]
Vậy, hệ số \( m \) là \( -5 \).
#### c) Tìm \( m \) để đường thẳng \( y = mx - 5 \) có đúng một điểm chung với \( y = \frac{1}{2} x^2 \)
Để tìm \( m \) để đường thẳng \( y = mx - 5 \) có đúng một điểm chung với parabol \( y = \frac{1}{2} x^2 \), ta giải hệ phương trình:
\[ \frac{1}{2} x^2 = mx - 5 \]
\[ \frac{1}{2} x^2 - mx + 5 = 0 \]
Phương trình này có đúng một nghiệm khi và chỉ khi nó có nghiệm kép, tức là delta (\( \Delta \)) bằng 0:
\[ \Delta = b^2 - 4ac \]
Ở đây, \( a = \frac{1}{2} \), \( b = -m \), và \( c = 5 \):
\[ \Delta = (-m)^2 - 4 \cdot \frac{1}{2} \cdot 5 \]
\[ \Delta = m^2 - 10 \]
Để phương trình có nghiệm kép:
\[ \Delta = 0 \]
\[ m^2 - 10 = 0 \]
\[ m^2 = 10 \]
\[ m = \pm \sqrt{10} \]
Vậy, \( m \) để đường thẳng \( y = mx - 5 \) có đúng một điểm chung với parabol \( y = \frac{1}{2} x^2 \) là \( m = \sqrt{10} \) hoặc \( m = -\sqrt{10} \).
### Bài 7
#### a) Vẽ đồ thị hàm số y=12x2𝑦=12𝑥2
Đồ thị của hàm số y=12x2𝑦=12𝑥2 là một parabol có đỉnh tại gốc tọa độ (0,0) và mở lên trên. Một số điểm để vẽ đồ thị bao gồm:
- Khi x=−2𝑥=−2, y=12(−2)2=2𝑦=12(−2)2=2
- Khi x=−1𝑥=−1, y=12(−1)2=12𝑦=12(−1)2=12
- Khi x=0𝑥=0, y=0𝑦=0
- Khi x=1𝑥=1, y=12(1)2=12𝑦=12(1)2=12
- Khi x=2𝑥=2, y=12(2)2=2𝑦=12(2)2=2
Sử dụng các điểm này, chúng ta có thể vẽ đồ thị của hàm số y=12x2𝑦=12𝑥2.
không vẽ hình
#### b) Xác định hệ số m biết rằng đường thẳng y=mx−5𝑦=𝑚𝑥−5 đi qua điểm A(−1,0)𝐴(−1,0)
Điểm A(−1,0)𝐴(−1,0) nằm trên đường thẳng y=mx−5𝑦=𝑚𝑥−5. Thay x=−1𝑥=−1 và y=0𝑦=0 vào phương trình của đường thẳng để tìm m𝑚:
0=m(−1)−50=𝑚(−1)−5
0=−m−50=−𝑚−5
m=−5𝑚=−5
Vậy, hệ số m𝑚 là −5−5.
#### c) Tìm m𝑚 để đường thẳng y=mx−5𝑦=𝑚𝑥−5 có đúng một điểm chung với y=12x2𝑦=12𝑥2
Để tìm m𝑚 để đường thẳng y=mx−5𝑦=𝑚𝑥−5 có đúng một điểm chung với parabol y=12x2𝑦=12𝑥2, ta giải hệ phương trình:
12x2=mx−512𝑥2=𝑚𝑥−5
12x2−mx+5=012𝑥2−𝑚𝑥+5=0
Phương trình này có đúng một nghiệm khi và chỉ khi nó có nghiệm kép, tức là delta (ΔΔ) bằng 0:
Δ=b2−4acΔ=𝑏2−4𝑎𝑐
Ở đây, a=12𝑎=12, b=−m𝑏=−𝑚, và c=5𝑐=5:
Δ=(−m)2−4⋅12⋅5Δ=(−𝑚)2−4⋅12⋅5
Δ=m2−10Δ=𝑚2−10
Để phương trình có nghiệm kép:
Δ=0Δ=0
m2−10=0𝑚2−10=0
m2=10𝑚2=10
m=±√10𝑚=±10
Vậy, m𝑚 để đường thẳng y=mx−5𝑦=𝑚𝑥−5 có đúng một điểm chung với parabol y=12x2𝑦=12𝑥2 là m=√10𝑚=10 hoặc m=−√10𝑚=−10.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


