Quảng cáo
2 câu trả lời 187
a) Đồ thị \( y = x^2 \)
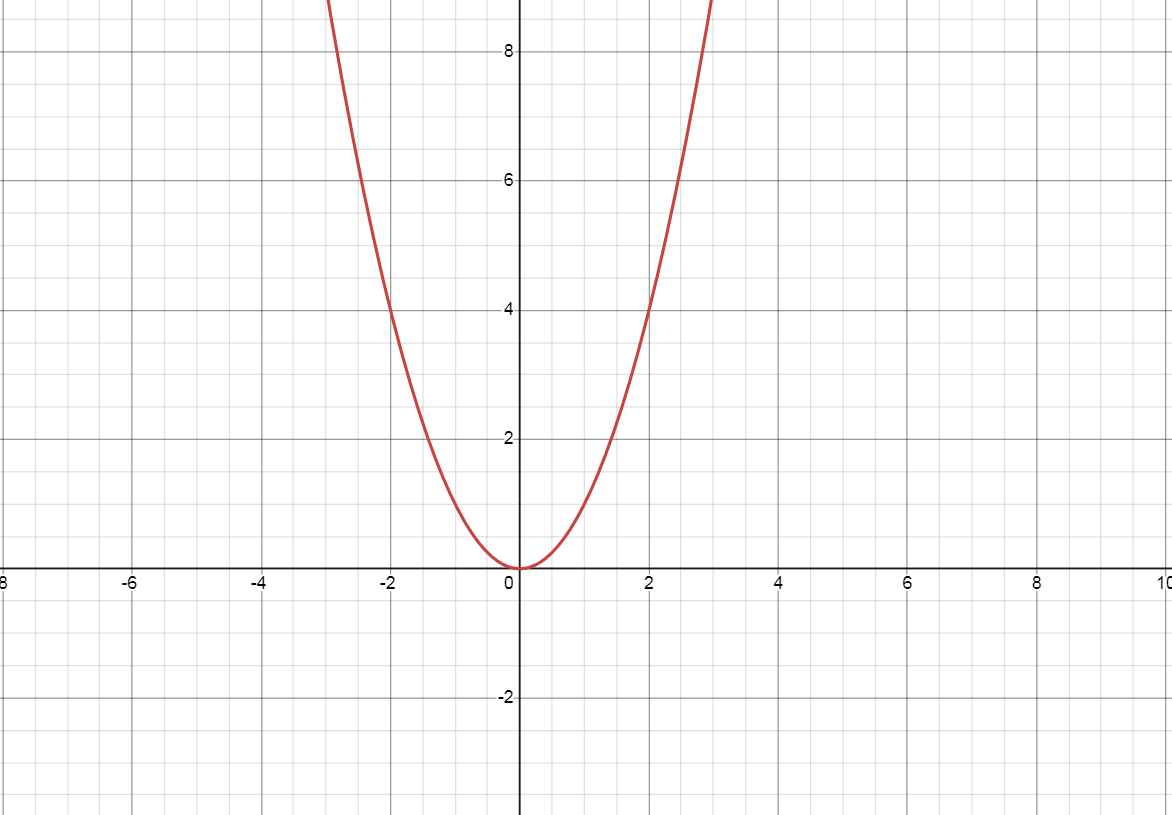
b) Để chứng minh rằng đường thẳng \( (d): y = mx - m + 1 \) cắt đồ thị của hàm số \( y = x^2 \) tại hai điểm phân biệt \( A \) và \( B \) với \( A(2, 1) \) bất kỳ giá trị nào của \( m \), chúng ta cần thực hiện các bước sau:
### 1. Xác định điểm cắt của \( (d) \) và \( y = x^2 \):
Phương trình đường thẳng \( (d) \) là:
\[ y = mx - m + 1 \]
Phương trình hàm số \( (1) \) là:
\[ y = x^2 \]
### 2. Giải phương trình hoành độ giao điểm:
Để tìm giao điểm của đường thẳng và parabol, ta giải hệ phương trình:
\[ x^2 = mx - m + 1 \]
Chuyển tất cả các thành phần về một phía:
\[ x^2 - mx + m - 1 = 0 \]
### 3. Xác định điểm \( A(2, 1) \):
Giả sử \( x = 2 \) là nghiệm của phương trình:
\[ 2^2 - 2m + m - 1 = 0 \]
\[ 4 - 2m + m - 1 = 0 \]
\[ 3 - m = 0 \]
\[ m = 3 \]
### 4. Chứng minh phương trình có hai nghiệm phân biệt với mọi giá trị của \( m \):
Để phương trình \( x^2 - mx + m - 1 = 0 \) có hai nghiệm phân biệt, điều kiện cần và đủ là:
\[ \Delta > 0 \]
Ta có:
\[ \Delta = b^2 - 4ac = (-m)^2 - 4 \cdot 1 \cdot (m - 1) \]
\[ \Delta = m^2 - 4(m - 1) \]
\[ \Delta = m^2 - 4m + 4 \]
\[ \Delta = (m - 2)^2 \]
### 5. Đánh giá điều kiện của \( \Delta \):
Bình phương của một số thực luôn không âm, nên:
\[ \Delta = (m - 2)^2 \geq 0 \]
\[
\text{Điều này có nghĩa là phương trình } x^2 - mx + m - 1 = 0 \text{ luôn có hai nghiệm phân biệt hoặc trùng. Tuy nhiên, để có hai điểm phân biệt, } \Delta > 0 \text{, tức } (m - 2)^2 \neq 0 \text{ ( } m \neq 2).
\]
### 6. Kết luận:
Vậy với mọi giá trị của \( m \) (trừ \( m = 2 \)), đường thẳng \( y = mx - m + 1 \) sẽ cắt parabol \( y = x^2 \) tại hai điểm phân biệt \( A \) và \( B \).
Điểm \( A \) có tọa độ \( (2, 1) \) khi \( m = 3 \), còn điểm \( B \) phụ thuộc vào giá trị của \( m \).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


