a) Tính đồng biến và nghịch biến:

Hàm số \( y = x^2 \) là một hàm số bậc hai. Trong đoạn \( (-\infty, 0) \), hàm số này là đồng biến tăng vì \( y \) tăng khi \( x \) giảm. Trong đoạn \( (0, +\infty) \), hàm số này là đồng biến giảm vì \( y \) giảm khi \( x \) tăng. Do đó, hàm số \( y = x^2 \) là đồng biến tăng trên đoạn \( (-\infty, 0) \) và đồng biến giảm trên đoạn \( (0, +\infty) \).

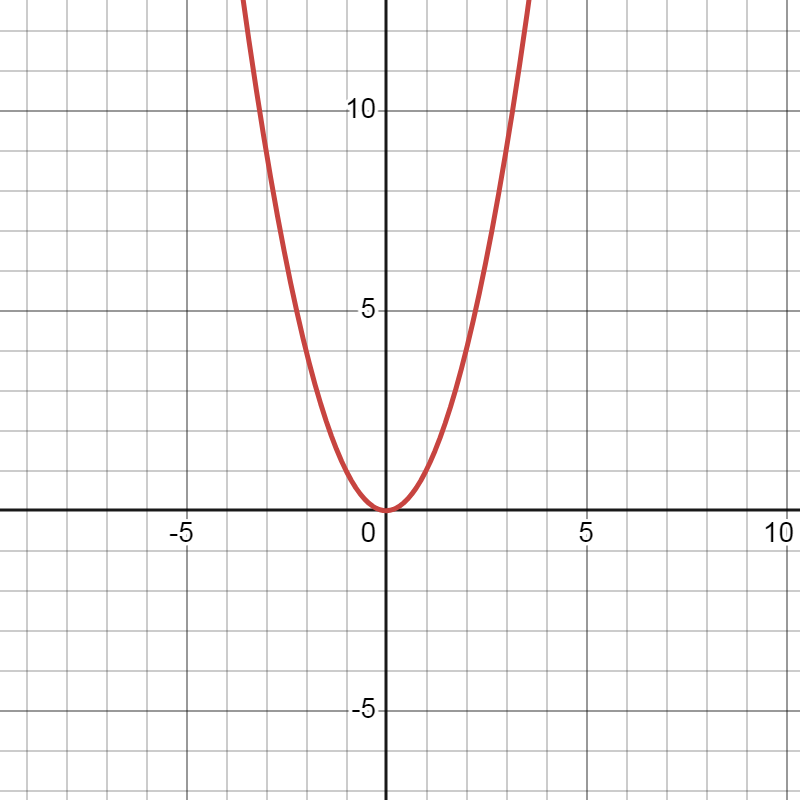
b) Vẽ đồ thị của hàm số \( y = x^2 \):

Đồ thị của hàm số \( y = x^2 \) là một parabol mở lên, với đỉnh ở gốc tọa độ.

c) Tìm các điểm \( A \) và \( B \):

Điểm \( A \) có hoành độ \( x = -4 \), do đó \( y = (-4)^2 = 16 \). Vậy điểm \( A \) có tọa độ \( (-4, 16) \).

Điểm \( B \) có tung độ \( y = 9 \), do đó \( x = \sqrt{9} = \pm 3 \). Vì đề bài không chỉ định rõ, nên ta sẽ có hai điểm \( B \) với hoành độ \( x = 3 \) và \( x = -3 \). Vậy các điểm \( B \) có tọa độ là \( (-3, 9) \) và \( (3, 9) \).

d) Tìm tọa độ của giao điểm giữa parabol \( y = x^2 \) và đường thẳng \( y = -2x + 3 \):

Để tìm điểm giao nhau giữa hai đồ thị, ta giải hệ phương trình:

\[ x^2 = -2x + 3 \]

\[ x^2 + 2x - 3 = 0 \]

Đây là một phương trình bậc hai, ta có thể giải bằng cách sử dụng công thức giải phương trình bậc hai:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Với \( a = 1 \), \( b = 2 \), và \( c = -3 \), ta có:

\[ x = \frac{-2 \pm \sqrt{2^2 - 4 \cdot 1 \cdot (-3)}}{2 \cdot 1} \]

\[ x = \frac{-2 \pm \sqrt{4 + 12}}{2} \]

\[ x = \frac{-2 \pm \sqrt{16}}{2} \]

\[ x = \frac{-2 \pm 4}{2} \]

Vậy ta có hai giá trị của \( x \):

\[ x_1 = \frac{-2 + 4}{2} = \frac{2}{2} = 1 \]

\[ x_2 = \frac{-2 - 4}{2} = \frac{-6}{2} = -3 \]

Khi \( x = 1 \), ta có \( y = (1)^2 = 1 \), nên điểm giao nhau là \( (1, 1) \).
Khi \( x = -3 \), ta có \( y = (-3)^2 = 9 \), nên điểm giao nhau là \( (-3, 9) \).

Vậy hai tọa độ giao điểm giữa parabol \( y = x^2 \) và đường thẳng \( y = -2x + 3 \) là \( (1, 1) \) và \( (-3, 9) \).

a. Để xác định tính đồng biến và nghịch biến của hàm số y = x², ta cần xem xét đạo hàm của hàm số này. Đạo hàm của y = x² là y' = 2x.
- Hàm số y = x² đồng biến trên một khoảng nếu đạo hàm của nó không âm trên khoảng đó.
- Hàm số y = x² nghịch biến trên một khoảng nếu đạo hàm của nó không dương trên khoảng đó.

Vì đạo hàm của y = x² là y' = 2x luôn không âm trên toàn bộ miền xác định, nên hàm số y = x² là hàm số đồng biến trên toàn bộ miền xác định.

b. Đồ thị của hàm số y = x² là một parabol mở lên, đi qua gốc tọa độ (0,0).

c. Để tìm các điểm A và B trên đồ thị y = x², ta thay hoành độ x của điểm A vào phương trình y = x² để tìm tung độ, và thay tung độ y của điểm B vào phương trình để tìm hoành độ.
- Điểm A: A(-4, (-4)²) = A(-4, 16)
- Điểm B: B(±√9, 9) = B(-3, 9) hoặc B(3, 9)

d. Để tìm tọa độ giao điểm của parabol y = x² với đường thẳng y = -2x + 3, ta giải hệ phương trình:
x² = -2x + 3
x² + 2x - 3 = 0
(x + 3)(x - 1) = 0
=> x = -3 hoặc x = 1

Khi x = -3, y = (-3)² = 9
Khi x = 1, y = 1² = 1

Vậy tọa độ giao điểm của parabol y = x² với đường thẳng y = -2x + 3 là (-3, 9) và (1, 1).