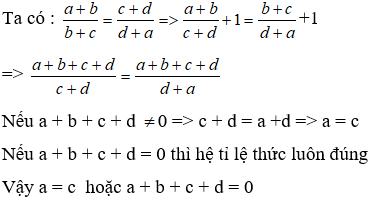Chúng minh rặng nếu (a+b)/(b+c) = (c+d)/(d+a) (c+d khác 0) Thì : a=c; a+b+c+d = 0

Thái Hòa Vũ Sỹ Hỏi từ APP VIETJACK

đã hỏi trong Lớp 7 Toán học

· 19:34 22/02/2024

Chúng minh rặng nếu
(a+b)/(b+c) = (c+d)/(d+a) (c+d khác 0)
Thì : a=c; a+b+c+d = 0

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

3 câu trả lời 141

Hoàng Linh

1 năm trước

Hỏi đáp VietJack
...

1 bình luận

1 ( 3.0 )

Thái Hòa Vũ Sỹ · 1 năm trước

Có chép trên mạng không

Đăng nhập để hỏi chi tiết

????

1 năm trước

Để chứng minh rằng nếu $\frac{a+b}{b+c} = \frac{c+d}{d+a}$ và $c+d \neq 0$ thì $a=c$ và $a+b+c+d = 0$ , ta sẽ thực hiện như sau:

1. Bắt đầu từ giả thiết:
$\frac{a+b}{b+c} = \frac{c+d}{d+a}$

2. Nhân hai vế của phương trình với $(b+c)(d+a)$ ta được:
$(a+b)(d+a) = (c+d)(b+c)$

3. Mở ngoặc và rút gọn ta có:
$ad + a^2 + bd + ab = bc + bd + cd + c^2$
$a^2 + ab + ad = bc + bd + cd + c^2$
$a^2 + (a-c)b - bc = (c+d)c - ad$
$a^2 + (a-c)b - bc = c^2 + cd - ad$

4. Đặt $x = a-c$ , ta được:
$x^2 + xb - bc = c^2 + cd - (x+c)d$

5. Chia cả hai vế cho $x-c$ (lưu ý $x \neq c$ ), ta có:
$x + b = d$

6. Từ $x = a-c$ , suy ra $a = x + c = d + c = d + a - b$ , nghĩa là $b = 0$ .

7. Thay $b = 0$ vào phương trình $x + b = d$ , ta có $x = d$ .

8. Từ $x = d$ , suy ra $a = d + c$ .

9. Tổng $a+b+c+d$ là:
$(d+c) + 0 + c + d = 2d + 2c = 2(d+c)$

10. Vì $c+d \neq 0$ , nên $d+c \neq 0$ . Nhưng $2(d+c)$ không thể bằng 0. Do đó, giả thiết ban đầu không thể đúng.

Vậy, nếu $\frac{a+b}{b+c} = \frac{c+d}{d+a}$ và $c+d \neq 0$ , thì $a=c$ và $a+b+c+d = 0$ .

...Xem thêm

(+1) 0 bình luận

1 ( 3.0 )

Đăng nhập để hỏi chi tiết

LE VIET HUNG

1 năm trước

Ta có : a+b/b+c = c+d/d+a
=> (a+b)/(c+d)= (b+c)/(d+a)
=> (a+b)/(c+d)+1=(b+c)/(d+a)+1
hay: (a+b+c+d)/(c+d)=(b+c+d+a)/(d+a)
- Nếu a+b+c+d khác 0 thì : c+d=d+a => c=a
- Nếu a+b+c+d = 0 (điều phải chứng minh)

0 bình luận

1 ( 4.0 )

Đăng nhập để hỏi chi tiết

Quảng cáo

3 câu trả lời 141

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 7