Cho có AB < AC. Kẻ tia phân giác AD của (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a)
b) F, D E thẳng hàng;
c)
Quảng cáo
20 câu trả lời 128030
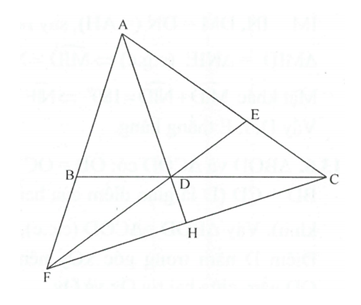
a) chứng minh tam giác ABC= tam giác EDC
b) chứng minh AB//DE
Cho có AB < AC. Kẻ tia phân giác AD của (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a)
b) F, D E thẳng hàng;
c)
Cho có AB < AC. Kẻ tia phân giác AD của (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a)
b) F, D E thẳng hàng;
c)
1 . Theo em , đối với người thợ mộc , ba trăm quan tiền có phải là số tiền lớn không ? Căn cứ vào đâu để khẳng định như vậy ?
2. Chi tiết người thợ mộc bỏ ra ba trăm quan tiền mua gỗ thể hiện điều gì ?
3. Vì sao những lời góp ý của người qua đường không giúp người thợ mộc bán được cày ?
4. Đặt một câu có sử dụng thành ngữ đẽo cày giữa đường .
5 . Em hãy tìm một thành ngữ có ý nghĩa tương tự thành ngữ đẽo cày giữa đường.
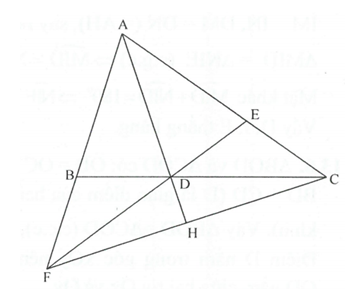
Cho ΔABC𝛥𝐴𝐵𝐶 có AB < AC. Kẻ tia phân giác AD của ˆBAC𝐵𝐴𝐶^ (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a) ΔBDF=ΔEDC;𝛥𝐵𝐷𝐹=𝛥𝐸𝐷𝐶;
b) F, D E thẳng hàng;
c) AD⊥FC
Quảng cáo
Câu hỏi hot cùng chủ đề
-
6 65237
-
Hỏi từ APP VIETJACK6 40522
-
9 40191
Bài viết mới nhất Lớp 7
-
1 năm trước2137
