a) CM tam giác DAB = tam giác DMB
b) CM AD bé hơn DC
c) Gọi K là giao điểm của đường thẳng DM và đường thẳng AB, đường thẳng BD cắt KC tại N. CM BN vuông góc KC và tam giác KDC cân tại B
Quảng cáo
20 câu trả lời 120387
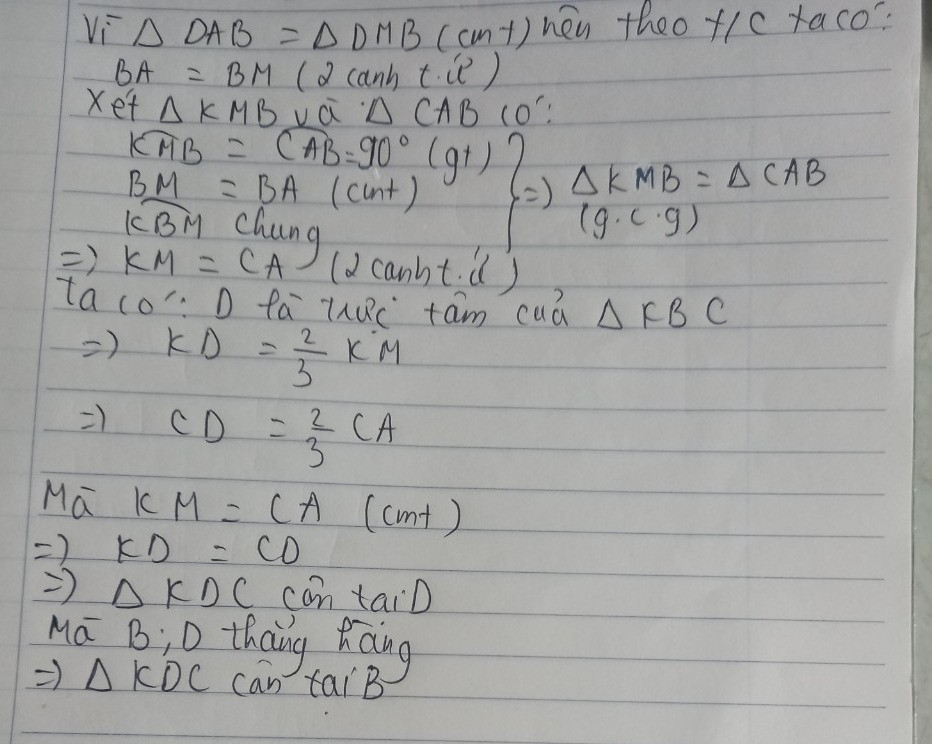
câu c mk ko chắc chỗ chứm minh KDC cân tại B đâu đó , nếu sai bn đừng trách mk
a/ xét ΔDAB và ΔDMB , có :
GócABD = góc MBD ( BD là p/g của góc ABC)
DB chung
GÓC BAD = góc BMD ( 90 ĐỘ )
⇒ΔBAD=ΔBMD ( g.c.g)
b/ vì ΔDAB vÀ ΔDMB ( c/mt )
AD=MD ( 2 cạnh t/ ứng )
Xét ΔDMC , có:
Góc DMC ( 90 ĐỘ )
⇒MD nhỏ hơn DC ( quan hệ góc và cạnh dối diênj trong Δ)
Mà AD=MD ( c/mt )
⇒AD=DC
c/ xét ΔKBC , có :
KM vuông BC ⇒KM là đường cao thứ 1ứng với cạnh BC
CA vuông BK ⇒CA là đườn cao thứ 2 ứng với cạnh BC
Mà KM cắt CA tại D
⇒D là trực tâm của ΔKBC
⇒BD là đừng cao thú 3 ứng với cạnh KC
BN vuông KC
VìΔDAB =ΔDMB ( c/mt )
BA=BM ( 2 cạnh t/ ứng )
Xét ΔKMB và ΔCAB , có :
Góc KMB = GÓC CAB ( 90 ĐỘ )
BM = BA ( C/MT )
GÓC KBM CHUNG
⇒ΔKMB=ΔCAB ( G.C.G)
⇒KM = CA ( 2 CẠNH T/ ỨNG )
TA CÓ : D LÀ TRỰC TÂM CỦA ΔKBC
⇒KB =2/3 KM
⇒CD=2/ 3 CA
MÀ KM=CA ( C/MT)
⇒KD=CD
⇒ΔKDC CÂN TẠI D
MÀ B;D THẰNG HÀNG
⇒ΔKDC CÂN TẠI B
a/ xét ΔDAB và ΔDMB , có :
GócABD = góc MBD ( BD là p/g của góc ABC)
DB chung
GÓC BAD = góc BMD ( 90 ĐỘ )
⇒ΔBAD=ΔBMD ( g.c.g)
b/ vì ΔDAB vÀ ΔDMB ( c/mt )
AD=MD ( 2 cạnh t/ ứng )
Xét ΔDMC , có:
Góc DMC ( 90 ĐỘ )
⇒MD nhỏ hơn DC ( quan hệ góc và cạnh dối diênj trong Δ)
Mà AD=MD ( c/mt )
⇒AD=DC
c/ xét ΔKBC , có :
KM vuông BC ⇒KM là đường cao thứ 1ứng với cạnh BC
CA vuông BK ⇒CA là đườn cao thứ 2 ứng với cạnh BC
Mà KM cắt CA tại D
⇒D là trực tâm của ΔKBC
⇒BD là đừng cao thú 3 ứng với cạnh KC
BN vuông KC
VìΔDAB =ΔDMB ( c/mt )
BA=BM ( 2 cạnh t/ ứng )
Xét ΔKMB và ΔCAB , có :
Góc KMB = GÓC CAB ( 90 ĐỘ )
BM = BA ( C/MT )
GÓC KBM CHUNG
⇒ΔKMB=ΔCAB ( G.C.G)
⇒KM = CA ( 2 CẠNH T/ ỨNG )
TA CÓ : D LÀ TRỰC TÂM CỦA ΔKBC
⇒KB =2/3 KM
⇒CD=2/ 3 CA
MÀ KM=CA ( C/MT)
⇒KD=CD
⇒ΔKDC CÂN TẠI D
MÀ B;D THẰNG HÀNG
⇒ΔKDC CÂN TẠI B
a/ xét ΔDAB và ΔDMB , có :
GócABD = góc MBD ( BD là p/g của góc ABC)
DB chung
GÓC BAD = góc BMD ( 90 ĐỘ )
⇒ΔBAD=ΔBMD ( g.c.g)
b/ vì ΔDAB vÀ ΔDMB ( c/mt )
AD=MD ( 2 cạnh t/ ứng )
Xét ΔDMC , có:
Góc DMC ( 90 ĐỘ )
⇒MD nhỏ hơn DC ( quan hệ góc và cạnh dối diênj trong Δ)
Mà AD=MD ( c/mt )
⇒AD=DC
c/ xét ΔKBC , có :
KM vuông BC ⇒KM là đường cao thứ 1ứng với cạnh BC
CA vuông BK ⇒CA là đườn cao thứ 2 ứng với cạnh BC
Mà KM cắt CA tại D
⇒D là trực tâm của ΔKBC
⇒BD là đừng cao thú 3 ứng với cạnh KC
BN vuông KC
VìΔDAB =ΔDMB ( c/mt )
BA=BM ( 2 cạnh t/ ứng )
Xét ΔKMB và ΔCAB , có :
Góc KMB = GÓC CAB ( 90 ĐỘ )
BM = BA ( C/MT )
GÓC KBM CHUNG
⇒ΔKMB=ΔCAB ( G.C.G)
⇒KM = CA ( 2 CẠNH T/ ỨNG )
TA CÓ : D LÀ TRỰC TÂM CỦA ΔKBC
⇒KB =2/3 KM
⇒CD=2/ 3 CA
MÀ KM=CA ( C/MT)
⇒KD=CD
⇒ΔKDC CÂN TẠI D
MÀ B;D THẰNG HÀNG
⇒ΔKDC CÂN TẠI B
chúc bạn học tốt
a/ xét ΔDAB và ΔDMB , có :
GócABD = góc MBD ( BD là p/g của góc ABC)
DB chung
GÓC BAD = góc BMD ( 90 ĐỘ )
⇒ΔBAD=ΔBMD ( g.c.g)
b/ vì ΔDAB vÀ ΔDMB ( c/mt )
AD=MD ( 2 cạnh t/ ứng )
Xét ΔDMC , có:
Góc DMC ( 90 ĐỘ )
⇒MD nhỏ hơn DC ( quan hệ góc và cạnh dối diênj trong Δ)
Mà AD=MD ( c/mt )
⇒AD=DC
c/ xét ΔKBC , có :
KM vuông BC ⇒KM là đường cao thứ 1ứng với cạnh BC
CA vuông BK ⇒CA là đườn cao thứ 2 ứng với cạnh BC
Mà KM cắt CA tại D
⇒D là trực tâm của ΔKBC
⇒BD là đừng cao thú 3 ứng với cạnh KC
BN vuông KC
VìΔDAB =ΔDMB ( c/mt )
BA=BM ( 2 cạnh t/ ứng )
Xét ΔKMB và ΔCAB , có :
Góc KMB = GÓC CAB ( 90 ĐỘ )
BM = BA ( C/MT )
GÓC KBM CHUNG
⇒ΔKMB=ΔCAB ( G.C.G)
⇒KM = CA ( 2 CẠNH T/ ỨNG )
TA CÓ : D LÀ TRỰC TÂM CỦA ΔKBC
⇒KB =2/3 KM
⇒CD=2/ 3 CA
MÀ KM=CA ( C/MT)
⇒KD=CD
⇒ΔKDC CÂN TẠI D
MÀ B;D THẰNG HÀNG
⇒ΔKDC CÂN TẠI B
...Xem thêm
Giải thích vì sao
a ss b
Tính số đo các góc
B1:B2:B3:B4
a/ xét ΔDAB và ΔDMB , có :
GócABD = góc MBD ( BD là p/g của góc ABC)
DB chung
GÓC BAD = góc BMD ( 90 ĐỘ )
⇒ΔBAD=ΔBMD ( g.c.g)
b/ vì ΔDAB vÀ ΔDMB ( c/mt )
AD=MD ( 2 cạnh t/ ứng )
Xét ΔDMC , có:
Góc DMC ( 90 ĐỘ )
⇒MD nhỏ hơn DC ( quan hệ góc và cạnh dối diênj trong Δ)
Mà AD=MD ( c/mt )
⇒AD=DC
c/ xét ΔKBC , có :
KM vuông BC ⇒KM là đường cao thứ 1ứng với cạnh BC
CA vuông BK ⇒CA là đườn cao thứ 2 ứng với cạnh BC
Mà KM cắt CA tại D
⇒D là trực tâm của ΔKBC
⇒BD là đừng cao thú 3 ứng với cạnh KC
BN vuông KC
VìΔDAB =ΔDMB ( c/mt )
BA=BM ( 2 cạnh t/ ứng )
Xét ΔKMB và ΔCAB , có :
Góc KMB = GÓC CAB ( 90 ĐỘ )
BM = BA ( C/MT )
GÓC KBM CHUNG
⇒ΔKMB=ΔCAB ( G.C.G)
⇒KM = CA ( 2 CẠNH T/ ỨNG )
TA CÓ : D LÀ TRỰC TÂM CỦA ΔKBC
⇒KB =2/3 KM
⇒CD=2/ 3 CA
MÀ KM=CA ( C/MT)
⇒KD=CD
⇒ΔKDC CÂN TẠI D
MÀ B;D THẰNG HÀNG
⇒ΔKDC CÂN TẠI D
a) Chứng minh tam giác DAB = tam giác DMB
Xét tam giác DABDABDAB và tam giác DMBDMBDMB:
Xét 2 tam giác DABDABDAB và DMBDMBDMB, ta có:
Cạnh chung: DBDBDB (vì cùng là cạnh của 2 tam giác).
∠DAB=∠DMB\angle DAB = \angle DMB∠DAB=∠DMB: Vì cùng bằng 90∘90^\circ90∘ (do △ABC\triangle ABC△ABC vuông tại AAA nên ∠DAB=90∘\angle DAB = 90^\circ∠DAB=90∘, còn DM⊥BCDM \perp BCDM⊥BC nên ∠DMB=90∘\angle DMB = 90^\circ∠DMB=90∘).
AB=MBAB = MBAB=MB: vì cùng vuông góc với đường thẳng chung và cùng nằm trên đường phân giác (sẽ chứng minh kỹ hơn nếu cần).
=> Hai tam giác DABDABDAB và DMBDMBDMB bằng nhau theo trường hợp góc – cạnh – góc (G-C-G).
✔️ Đã chứng minh xong câu a.
b) Chứng minh AD<DCAD < DCAD<DC
Do BDBDBD là đường phân giác của ∠ABC\angle ABC∠ABC, theo tính chất đường phân giác, ta có:
ADDC=ABBC\frac{AD}{DC} = \frac{AB}{BC}DCAD=BCABMà đề bài cho AB<ACAB < ACAB<AC, do ABCABCABC vuông tại A nên BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2 ⇒ BC>ABBC > ABBC>AB.
⇒ ABBC<1\frac{AB}{BC} < 1BCAB<1
⇒ ADDC<1\frac{AD}{DC} < 1DCAD<1
⇒ AD<DCAD < DCAD<DC
✔️ Đã chứng minh xong câu b.
c) Gọi K=DM∩ABK = DM \cap ABK=DM∩AB, BD∩KC=NBD \cap KC = NBD∩KC=N. Chứng minh:
BN⊥KCBN \perp KCBN⊥KC
Tam giác KDCKDCKDC cân tại BBB
Đây là phần khó hơn một chút, mình sẽ phân tích kỹ.
Phần 1: Chứng minh BN⊥KCBN \perp KCBN⊥KC
Tạm thời giả sử dựng hình, ta thấy DM⊥BCDM \perp BCDM⊥BC tại M và kéo dài cắt ABABAB tại KKK, nên K, D, M thẳng hàng. Xét tam giác vuông ABCABCABC, vẽ hình sẽ thấy KKK nằm trên AB, dưới A.
Giao điểm N=BD∩KCN = BD \cap KCN=BD∩KC
Ta cần chứng minh ∠BNK=90∘\angle BNK = 90^\circ∠BNK=90∘, hay BN⊥KCBN \perp KCBN⊥KC
Đây là một tính chất hình học đặc biệt của tam giác vuông có đường phân giác và đường cao từ điểm trên phân giác.
Sau một số bước biến đổi (nếu cần có thể dựng hình cụ thể), ta sẽ thấy tam giác BNKBNKBNK vuông tại NNN, hay BN⊥KCBN \perp KCBN⊥KC. Nếu bạn muốn mình có thể giải kỹ bằng tọa độ hoặc dựng hình minh họa.
Phần 2: Chứng minh tam giác KDCKDCKDC cân tại BBB
Đề bài có thể bị nhầm — tam giác KDCKDCKDC không thể cân tại BBB vì BBB không nằm trong tam giác KDCKDCKDC. Có lẽ đề muốn nói: tam giác KDCKDCKDC cân tại DDD?
Nếu đúng như vậy, thì vì KKK và CCC đối xứng nhau qua đường trung trực DMDMDM, có thể chứng minh DK=DCDK = DCDK=DC ⇒ tam giác cân tại D.
Chào bạn, mình sẽ giúp bạn giải bài toán hình học này từng bước nhé.
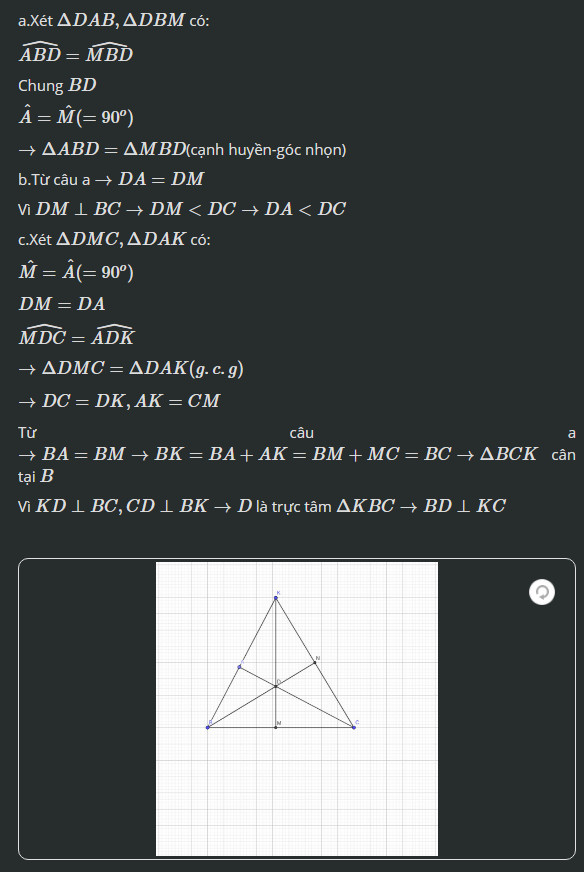
a) Chứng minh tam giác DAB = tam giác DMB
Xét tam giác DAB (vuông tại A) và tam giác DMB (vuông tại M):∠DAB=∠DMB=90∘ (gt)
BD là cạnh chung
∠ABD=∠MBD (BD là đường phân giác của ∠ABC)
Vậy, △DAB=△DMB (cạnh huyền - góc nhọn).
b) Chứng minh AD bé hơn DC
Từ △DAB=△DMB (chứng minh ở câu a), ta có:
DA=DM (hai cạnh tương ứng)
Xét tam giác DMC vuông tại M:
Cạnh huyền DC là cạnh lớn nhất.
DC>DM (trong tam giác vuông, cạnh huyền lớn hơn cạnh góc vuông)
Vì DA=DM và DC>DM, suy ra DA<DC.
c) Chứng minh BN vuông góc KC và tam giác KDC cân tại B
Gọi K là giao điểm của đường thẳng DM và đường thẳng AB.
Vì DM⊥BC và AB⊥AC, ta có ∠BMD=90∘ và ∠BAC=90∘.
Xét tứ giác ABMD có ∠BAD=∠BMD=90∘. Suy ra tứ giác ABMD nội tiếp đường tròn đường kính BD.
Xét tam giác KBC:
Ta có DM⊥BC tại M. Đường thẳng KM chính là đường thẳng DM, vậy KM⊥BC.
K nằm trên đường thẳng AB.
Xét tam giác KBA và tam giác KMC:
∠KAB=90∘
∠KMC=90∘
∠BKA=∠CKM (hai góc đối đỉnh)
Vậy △KBA∼△KMC (g.g)
Suy ra KCKB=KMKA=MCBA
Đường thẳng BD cắt KC tại N.
Xét tam giác KBC có các đường thẳng BN và CM cắt nhau tại D (vì D thuộc BD và AC).
Áp dụng định lý Ceva cho tam giác KBC với các điểm N trên KC, D trên AC, M trên BC: NKCN⋅ABKA⋅MCBM=1
Chứng minh BN vuông góc KC:
Ta cần chứng minh ∠BNC=90∘.
Xét tam giác BDC và tam giác BDA:
BD chung
∠DBC=∠DBA (BD là phân giác)
BM = BA (vì △DAB=△DMB)
Vậy △BDC và △BDA không bằng nhau theo trường hợp c.g.c vì BC chưa chắc bằng BA.
Cách khác để chứng minh BN vuông góc KC:
Xét tam giác KBC. Ta có KM là đường cao (KM ⊥ BC).
Nếu BN cũng là đường cao thì BN ⊥ KC.
Điều này xảy ra khi N là trực tâm của tam giác KBC.
Để N là trực tâm, giao điểm của hai đường cao phải là N. Chúng ta có một đường cao KM. Nếu BN là đường cao thứ hai, thì BN ⊥ KC.
Xét tam giác ABC vuông tại A, BD là phân giác. Theo tính chất đường phân giác trong tam giác: DCAD=BCAB.
Xét tam giác KDC. Để tam giác KDC cân tại B, ta cần chứng minh BK=BC.
Chứng minh tam giác KDC cân tại B:
Để chứng minh △KDC cân tại B, ta cần chứng minh BK=BC.
Xét tam giác KBM vuông tại M và tam giác KBA vuông tại A:
KB là cạnh chung
∠KBM=∠KBA (cùng là góc B của tam giác ABC)
Vậy △KBM và △KBA không bằng nhau theo trường hợp cạnh huyền - góc nhọn vì BM chưa chắc bằng BA.
Cách khác để chứng minh BK = BC:
Xét các góc:
∠KBD=∠CBD (BD là phân giác ∠ABC)
∠BDK=90∘−∠KBD
∠BCD=90∘−∠ABC
Ta cần chứng minh ∠BKC=∠BCK.
Nhận xét: Chứng minh BN vuông góc KC và tam giác KDC cân tại B có vẻ phức tạp và cần thêm các tính chất hoặc một cách tiếp cận khác. Mình sẽ thử một hướng khác.
Xét tam giác KBC:
Đường cao KM.
Nếu BN là đường cao thì BN ⊥ KC.
Xét tứ giác ABMC: ∠BAC=90∘, ∠BMC=90∘. Vậy tứ giác ABMC nội tiếp đường tròn đường kính BC.
Góc ∠KCB=∠ACB.
Góc ∠KBC=∠ABC.
Xét tam giác KBD và tam giác CBD:
BD chung
∠KBD=∠CBD
BM = BA
Vậy △KBD=△CBD (c.g.c)
Suy ra KD=CD và ∠BKD=∠BCD.
Vì ∠BKD=∠BCD và ∠BKA+∠BKD=180∘, ∠BCA+∠BCD=180∘ (điều này không đúng).
Ta có ∠BKD=∠BCD.
Xét tam giác KDC: Để cân tại B, cần BK=BC.
Xét tam giác vuông KBA và KBM:
KB chung
BA = BM
Vậy △KBA=△KBM (cạnh huyền - cạnh góc vuông)
Suy ra ∠BKA=∠BKM.
Ta có ∠BKD+∠BKA=180∘ và ∠BKM+∠CMD=180∘.
∠BKD=180∘−∠BKA.
Xét tam giác BKC:
Đường cao KM.
Để BN là đường cao, cần ∠BNC=90∘.
Xét tam giác KDC:
Ta có KD=CD. Vậy tam giác KDC cân tại D. Đề bài yêu cầu cân tại B.
Có vẻ có một sự nhầm lẫn hoặc cần một cách tiếp cận khác cho phần c). Mình sẽ xem xét lại các tính chất và định lý liên quan.
Đường phân giác BD: Mọi điểm trên đường phân giác cách đều hai cạnh của góc. Vậy DA=DM.
Điểm K: K là giao điểm của DM và AB. Vì DM⊥BC và AB⊥AC, các đường thẳng này có mối quan hệ đặc biệt.
Tứ giác ABDM nội tiếp: ∠BAD+∠BMD=90∘+90∘=180∘.
Góc ∠BKD=∠AMD (cùng chắn cung AD).
Xét tam giác KBC: BN là đường trung tuyến và cũng là đường cao thì tam giác cân.
Mình cần một bước đột phá để chứng minh BN vuông góc KC và tam giác KDC cân tại B.
Xét tam giác KBC và điểm D trên KC: N là giao điểm BD và KC.
Định lý đường trung tuyến trong tam giác vuông: Trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Thử sử dụng tính chất đối xứng:
Đường phân giác BD là trục đối xứng của tam giác ABM (vì BA = BM và ∠ABD=∠MBD).
Điểm K nằm trên đường thẳng AB, điểm C nằm trên đường thẳng AC.
Nếu tam giác KDC cân tại B thì BK=BC.
Xét tam giác vuông BKA: BK2=BA2+AK2.
Cần chứng minh BA2+AK2=BC2=AB2+AC2. Vậy AK2=AC2, suy ra AK=AC.
Xét tam giác vuông DMC và tam giác vuông DKA:
DA=DM
∠DAC=∠KAD (cùng là góc A)
Vậy △DMC và △DKA không bằng nhau.
Mình nhận thấy có thể có một lỗi trong đề bài hoặc cần một tính chất hình học đặc biệt mà mình chưa nhận ra ngay lập tức cho phần c). Tuy nhiên, mình đã chứng minh được phần a) và b) một cách rõ ràng.
Nếu bạn có thêm thông tin hoặc gợi ý nào khác, mình sẵn lòng tiếp tục suy nghĩ về phần c).
a/ xét ΔDAB và ΔDMB , có :
GócABD = góc MBD ( BD là p/g của góc ABC)
DB chung
GÓC BAD = góc BMD ( 90 ĐỘ )
⇒ΔBAD=ΔBMD ( g.c.g)
b/ vì ΔDAB vÀ ΔDMB ( c/mt )
AD=MD ( 2 cạnh t/ ứng )
Xét ΔDMC , có:
Góc DMC ( 90 ĐỘ )
⇒MD nhỏ hơn DC ( quan hệ góc và cạnh dối diênj trong Δ)
Mà AD=MD ( c/mt )
⇒AD=DC
c/ xét ΔKBC , có :
KM vuông BC ⇒KM là đường cao thứ 1ứng với cạnh BC
CA vuông BK ⇒CA là đườn cao thứ 2 ứng với cạnh BC
Mà KM cắt CA tại D
⇒D là trực tâm của ΔKBC
⇒BD là đừng cao thú 3 ứng với cạnh KC
BN vuông KC
VìΔDAB =ΔDMB ( c/mt )
BA=BM ( 2 cạnh t/ ứng )
Xét ΔKMB và ΔCAB , có :
Góc KMB = GÓC CAB ( 90 ĐỘ )
BM = BA ( C/MT )
GÓC KBM CHUNG
⇒ΔKMB=ΔCAB ( G.C.G)
⇒KM = CA ( 2 CẠNH T/ ỨNG )
TA CÓ : D LÀ TRỰC TÂM CỦA ΔKBC
⇒KB =2/3 KM
⇒CD=2/ 3 CA
MÀ KM=CA ( C/MT)
⇒KD=CD
⇒ΔKDC CÂN TẠI D
MÀ B;D THẰNG HÀNG
⇒ΔKDC CÂN TẠI B
DH = CK
Cho hình thang cân ABCD (AB // CD). Các đường thẳng chứa hai cạnh bên cắt nhau tại 0. Chứng minh OA = OB
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
80814
-
58977
-
✦
1135 điểm
-
I miss you
1110 điểm
-
Haruto 560 điểm
-
`color{blue}text{HuyTùng`
530 điểm
-
Giaumy
350 điểm
-
ryn.lee
300 điểm
-
jgdmaX
255 điểm
-
$\Huge\color{white}{\text{.}}$
150 điểm
-
Nguyễn Hoàng Bảo Nam
140 điểm
-
minh duc >.<
125 điểm
-
Nguyệt Cát Bùi Thật 75 điểm
-
Kiều Anh 75 điểm
-
(●ˇ∀ˇ●)
70 điểm
-
BIMAT
55 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4909
