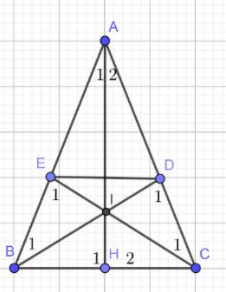
Cho ABC cân tại A (). Kẻ BD AC tại D, kẻ CE ⊥ AB tại E.
a) Chứng minh △ADE cân
b) chứng minh DE // BC
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC
d) Chứng minh AI ⊥ BC
Quảng cáo
6 câu trả lời 93194

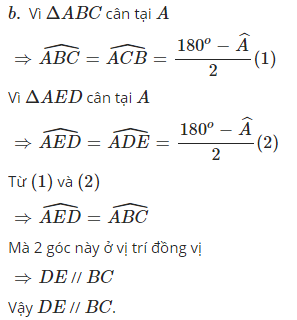
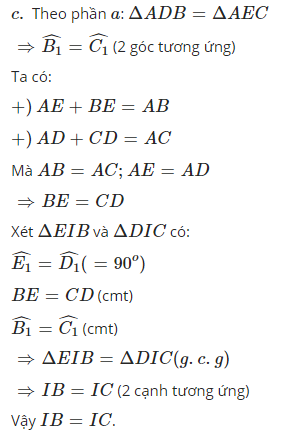

Bước 1: Chứng minh
△ADEtriangle cap A cap D cap E
△𝐴𝐷𝐸
cân
Xét hai tam giác vuông △ABDtriangle cap A cap B cap D
△𝐴𝐵𝐷
(vuông tại D) và △ACEtriangle cap A cap C cap E
△𝐴𝐶𝐸
(vuông tại E) có:
Cạnh huyền AB=ACcap A cap B equals cap A cap C
𝐴𝐵=𝐴𝐶
(do △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
cân tại A).
Góc ∠Aangle cap A
∠𝐴
là góc chung.
Do đó, △ABD≅△ACEtriangle cap A cap B cap D is congruent to triangle cap A cap C cap E
△𝐴𝐵𝐷≅△𝐴𝐶𝐸
(trường hợp cạnh huyền - góc nhọn) [1].
Từ sự đồng dạng trên, suy ra hai cạnh tương ứng bằng nhau: AD=AEcap A cap D equals cap A cap E
𝐴𝐷=𝐴𝐸
.
Trả lời:
Do AD=AEcap A cap D equals cap A cap E
𝐴𝐷=𝐴𝐸
, tam giác △ADEtriangle cap A cap D cap E
△𝐴𝐷𝐸
là tam giác cân tại A.
Bước 2: Chứng minh DE∥BCcap D cap E is parallel to cap B cap C
𝐷𝐸∥𝐵𝐶
Từ kết quả AD=AEcap A cap D equals cap A cap E
𝐴𝐷=𝐴𝐸
ở phần a), ta có tỉ số ADAC=AEABthe fraction with numerator cap A cap D and denominator cap A cap C end-fraction equals the fraction with numerator cap A cap E and denominator cap A cap B end-fraction
𝐴𝐷𝐴𝐶=𝐴𝐸𝐴𝐵
(vì AB=ACcap A cap B equals cap A cap C
𝐴𝐵=𝐴𝐶
).
Xét △ADEtriangle cap A cap D cap E
△𝐴𝐷𝐸
và △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
, chúng có góc ∠Aangle cap A
∠𝐴
chung và tỉ số các cạnh kề ADAC=AEABthe fraction with numerator cap A cap D and denominator cap A cap C end-fraction equals the fraction with numerator cap A cap E and denominator cap A cap B end-fraction
𝐴𝐷𝐴𝐶=𝐴𝐸𝐴𝐵
. Do đó, △ADE∼△ABCtriangle cap A cap D cap E tilde triangle cap A cap B cap C
△𝐴𝐷𝐸∼△𝐴𝐵𝐶
(trường hợp cạnh-góc-cạnh).
Từ sự đồng dạng này, ta suy ra các góc tương ứng bằng nhau, cụ thể là ∠ADE=∠ACBangle cap A cap D cap E equals angle cap A cap C cap B
∠𝐴𝐷𝐸=∠𝐴𝐶𝐵
.
Trả lời:
Hai góc ∠ADEangle cap A cap D cap E
∠𝐴𝐷𝐸
và ∠ACBangle cap A cap C cap B
∠𝐴𝐶𝐵
ở vị trí đồng vị bằng nhau nên DE∥BCcap D cap E is parallel to cap B cap C
𝐷𝐸∥𝐵𝐶
.
Bước 3: Chứng minh IB=ICcap I cap B equals cap I cap C
𝐼𝐵=𝐼𝐶
Ta có △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
cân tại A nên ∠ABC=∠ACBangle cap A cap B cap C equals angle cap A cap C cap B
∠𝐴𝐵𝐶=∠𝐴𝐶𝐵
.
Từ △ABD≅△ACEtriangle cap A cap B cap D is congruent to triangle cap A cap C cap E
△𝐴𝐵𝐷≅△𝐴𝐶𝐸
ở phần a), ta có ∠ABD=∠ACEangle cap A cap B cap D equals angle cap A cap C cap E
∠𝐴𝐵𝐷=∠𝐴𝐶𝐸
.
Trong △IBCtriangle cap I cap B cap C
△𝐼𝐵𝐶
, ta có các góc đáy:
∠IBC=∠ABC−∠ABDangle cap I cap B cap C equals angle cap A cap B cap C minus angle cap A cap B cap D
∠𝐼𝐵𝐶=∠𝐴𝐵𝐶−∠𝐴𝐵𝐷
∠ICB=∠ACB−∠ACEangle cap I cap C cap B equals angle cap A cap C cap B minus angle cap A cap C cap E
∠𝐼𝐶𝐵=∠𝐴𝐶𝐵−∠𝐴𝐶𝐸
Do ∠ABC=∠ACBangle cap A cap B cap C equals angle cap A cap C cap B
∠𝐴𝐵𝐶=∠𝐴𝐶𝐵
và ∠ABD=∠ACEangle cap A cap B cap D equals angle cap A cap C cap E
∠𝐴𝐵𝐷=∠𝐴𝐶𝐸
, suy ra ∠IBC=∠ICBangle cap I cap B cap C equals angle cap I cap C cap B
∠𝐼𝐵𝐶=∠𝐼𝐶𝐵
.
Trả lời:
Tam giác △IBCtriangle cap I cap B cap C
△𝐼𝐵𝐶
có hai góc đáy bằng nhau ( ∠IBC=∠ICBangle cap I cap B cap C equals angle cap I cap C cap B
∠𝐼𝐵𝐶=∠𝐼𝐶𝐵
) nên nó là tam giác cân tại I, suy ra IB=ICcap I cap B equals cap I cap C
𝐼𝐵=𝐼𝐶
.
Bước 4: Chứng minh AI⟂BCcap A cap I ⟂ cap B cap C
𝐴𝐼⟂𝐵𝐶
Icap I
𝐼
là giao điểm của hai đường cao BDcap B cap D
𝐵𝐷
và CEcap C cap E
𝐶𝐸
của △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
. Do đó, Icap I
𝐼
là trực tâm của tam giác △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
.
Đường thẳng AIcap A cap I
𝐴𝐼
đi qua đỉnh Acap A
𝐴
và trực tâm Icap I
𝐼
nên AIcap A cap I
𝐴𝐼
phải là đường cao thứ ba của △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
.
Trả lời:
Vì AIcap A cap I
𝐴𝐼
là đường cao của △ABCtriangle cap A cap B cap C
△𝐴𝐵𝐶
hạ xuống cạnh BCcap B cap C
𝐵𝐶
, nên AI⟂BCbold cap A bold cap I ⟂ bold cap B bold cap C
𝐀𝐈⟂𝐁𝐂
.
Cho △ABC cân tại A, A^<90∘\widehat A < 90^\circA<90∘. Kẻ BD⊥ACBD \perp ACBD⊥AC tại D, CE⊥ABCE \perp ABCE⊥AB tại E.
a) Vì AB=ACAB = ACAB=AC, lại có ADADAD chung và ∠BAD=∠DAE\angle BAD = \angle DAE∠BAD=∠DAE (do tam giác cân tại A), suy ra △ADE cân.
b) Ta có ∠ADE=∠ACB\angle ADE = \angle ACB∠ADE=∠ACB (cùng phụ với ∠ADC\angle ADC∠ADC), nên DE//BCDE // BCDE//BC.
c) Gọi I là giao điểm của BD và CE. Vì △ABC cân tại A nên BD và CE đối xứng nhau qua trục đối xứng của tam giác, suy ra I nằm trên đường trung trực của BC. Do đó IB=ICIB = ICIB=IC.
d) Vì I nằm trên đường trung trực của BC nên AI⊥BCAI \perp BCAI⊥BC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK123004
-
 Đã trả lời bởi chuyên gia
83301
Đã trả lời bởi chuyên gia
83301 -
 Đã trả lời bởi chuyên gia
62585
Đã trả lời bởi chuyên gia
62585 -
 Đã trả lời bởi chuyên gia
40389
Đã trả lời bởi chuyên gia
40389 -
 Đã trả lời bởi chuyên gia
36693
Đã trả lời bởi chuyên gia
36693


