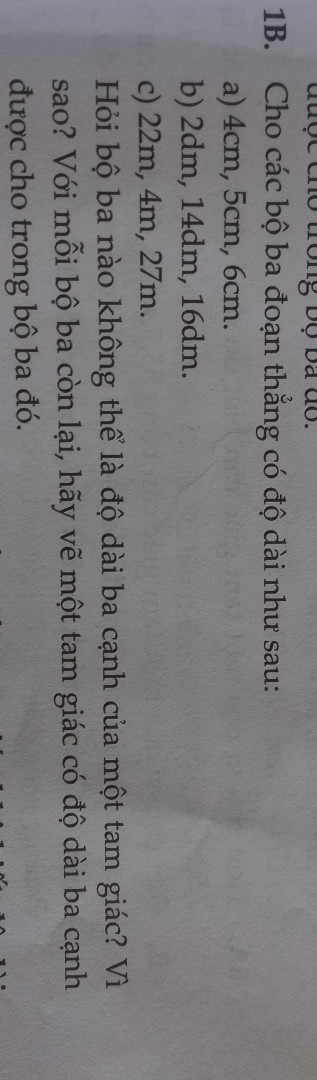Cho tam giác ABC có ba góc nhọn (AB<AC). Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao điểm của CD và BE, K là giao điểm của AB và DC.
a) Chứng minh rằng:
b) Chứng minh rằng:
c) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng đều
d) Chứng minh rằng IA+IB=ID
e) Chứng minh rằng IA là tia phân giác của góc DIE.
Quảng cáo
5 câu trả lời 59111
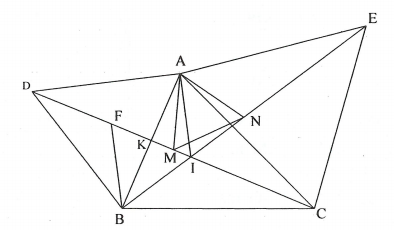
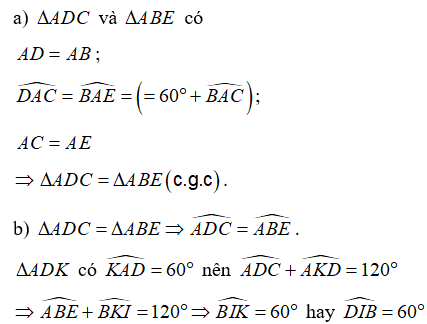
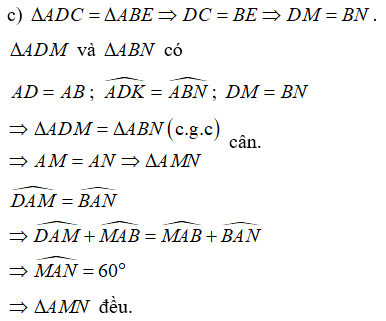
DAC BAE BAC 60= = +
Từ AD = AB; DAC BAE= và AC = AE
Suy ra ∆ADC = ∆ABE (c.g.c) 1,0
Từ ∆ADC = ∆ABE (câu a) ABE ADC⇒ = ,
mà BKI AKD= (đối đỉnh).
Khi đó xét ∆BIK và ∆DAK suy ra BIK DAK= = 600 (đpcm)
b) Từ ∆ADC = ∆ABE (câu a) ⇒ CM = EN và ACM AEN=
⇒∆ACM = ∆AEN (c.g.c) ⇒ AM = AN và CAM EAN=
MAN CAE= = 600. Do đó ∆AMN đều.
1,0
0,5
0,5
1,0
c) Trên tia ID lấy điểm J sao cho IJ = IB ⇒ ∆BIJ đều
⇒ BJ = BI và JBI DBA= = 600 suy ra IBA JBD= , kết hợp BA = BD
⇒∆IBA = ∆JBD (c.g.c)
AIB DJB⇒ = = 1200 mà BID = 600
DIA⇒ = 600. Từ đó suy ra IA là phân giác của góc DIE
vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv
a) +) Chứng minh ΔΔDAC = ΔΔBAE
Thật vậy: Ta có: AD = AB ( ΔΔDAB đều )
^DAB = ^CAE ( = 60oo; ΔΔDAB đều ; ΔΔCAE đều ) => ^DAC = ^BAE
CA = AE ( ΔΔCAE đều )
Từ 3 điều trên => ΔΔDAC = ΔΔBAE ( c.g.c) (1)
=> ^ABE = ^ADC (2)
+) Xét ΔΔKAD và ΔΔKIB có: ^DKA = ^BKI ( đối đỉnh )
^KDA = ^KBI( theo ( 2) )
mà ^DKA + ^KDA + ^KAD= ^BKI + ^KBI + ^KIB = 180oo
=> ^KIB = ^KAD = ^BAD= 60oo
=> ^DIB = 60oo
b) Từ (1) => DC = BE mà M là trung điểm DC; N là trung điểm BE
=> DM = BN (3)
+) Xét ΔΔBAN và ΔΔDAM
có: BN = DM ( theo (3)
^ABN = ^ADM ( theo (2)
AB = AD ( ΔΔADB đều )
=> ΔΔBAN = ΔΔDAM (4)
=> AN = AM => ΔΔAMN cân tại A (5)
+) Từ (4) => ^BAN = ^DAM => ^BAM + ^MAN = ^DAB + ^BAM
=> ^MAN = ^DAB = 60oo(6)
Từ (5); (6) => ΔΔAMN đều
c) +) Trên tia đối tia MI lấy điểm F sao cho FI = IB => ΔΔFIB cân tại I
mà ^BIF = ^BID = 60oo( theo (a))
=> ΔΔFIB đều (7)
=> ^DBA = ^FBI( =60oo)
=> ^DBF + ^FBA = ^FBA + ^ABI
=> ^DBF = ^ABI
Lại có: BI = BF ( theo (7) ) và BA = BD ( ΔΔBAD đều )
Từ (3) điều trên => ΔΔDFB = ΔΔAIB => ^AIB = ^DFB = 180oo- ^BFI = 180oo-60oo=120oo
+) Mặt khác ^BID = 60 oo( theo (a) )
=> ^DIE = 180oo- ^BID = 120 oovà ^DIA = ^AIB - ^BID = 120oo-60oo=60oo
=> ^AIE = ^DIE - ^DIA = 120oo-60oo=60oo
=> ^DIA = ^AIE ( = 60oo)
=> IA là phân giác ^DIE.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120267
-
80814
-
✦
1135 điểm
-
I miss you
1110 điểm
-
Haruto 560 điểm
-
`color{blue}text{HuyTùng`
530 điểm
-
Giaumy
350 điểm
-
ryn.lee
300 điểm
-
jgdmaX
255 điểm
-
$\Huge\color{white}{\text{.}}$
150 điểm
-
Nguyễn Hoàng Bảo Nam
140 điểm
-
minh duc >.<
125 điểm
-
Nguyệt Cát Bùi Thật 75 điểm
-
Kiều Anh 75 điểm
-
(●ˇ∀ˇ●)
70 điểm
-
BIMAT
55 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4909
