Cho hình bình hành ABCD, trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F. Sao cho, AE = CF. Trên cạnh BC lấy điểm G, cạnh AD lấy điểm H, sao cho BG = DH
a) Chứng minh tứ giác EGFH là hình bình hành
b) Chứng minh các đường thẳng AC, BD, EF, GH đồng quy
Quảng cáo
2 câu trả lời 1725
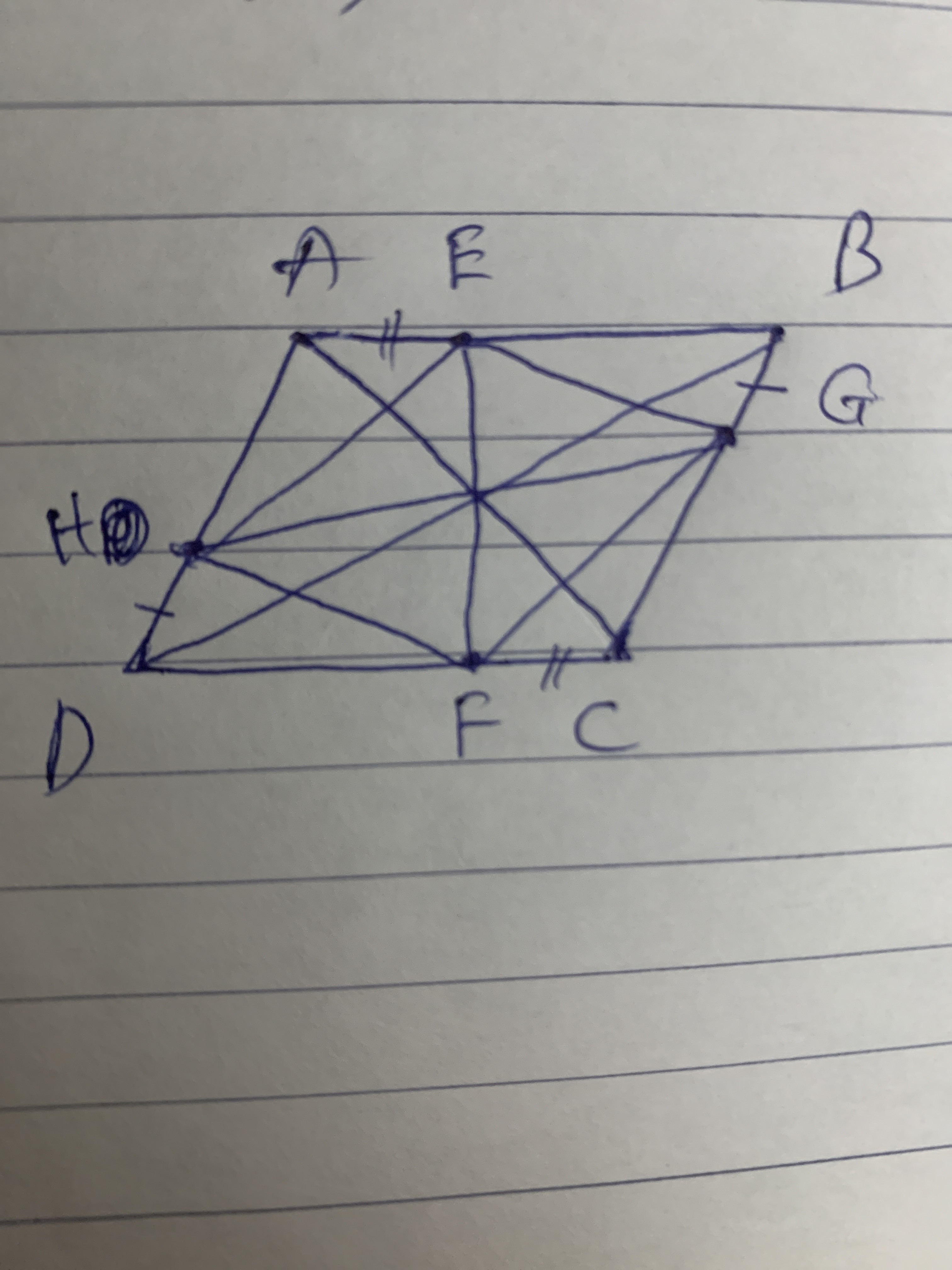
a) Vì ABCD là hình bình hành nên
góc HAE= góc GCF
và AD=BC.
Mà DH=BG
⇒AD−DH=BC−BG
hay AH=CG.
Xét △AHE và △CGF có:
+AE=CF (gt)
+góc HAE= góc GCF (cmt)
+AH=CG (cmt)
⇒△AHE=△CGF (c.g.c)
⇒HE=GF.
Cmtt: EG=FH.
Suy ra tứ giác EGFH là hình bình hành.
b)
Gọi O là giao điểm của AC và BD
⇒O là trung điểm của AC.
Tứ giác AECF có AE//CF;AE=CF nên là hình bình hành
⇒ Hai đường chéo AC và EF cắt nhau tại trung điểm mỗi đường.
Mà O là trung điểm của AC
⇒O là trung điểm của EF.
Tứ giác EGFH là hình bình hành nên
hai đường chéo EF và GH cắt nhau tại trung điểm mỗi đường.
Mà O là trung điểm của EF
⇒O là trung điểm của GH.
Vậy các đường thẳng AC,BD,EF,GH đồng quy tại O.
a: Xét ΔEBG và ΔFDH có
BE=DF
góc B=góc D
BG=DH
Do đó: ΔEBG=ΔFDH
Suy ra: EG=FH
Xét ΔAEH và ΔCFG có
AE=CF
góc EAH=góc FCG
AH=CG
Do đó: ΔAEH=ΔCFG
Suy ra: HE=FG
Xét tứ giác EGFH có
EG=FH
EH=GF
Do đó: EGFH là hình bình hành
b: Ta có: AECF là hình bình hành
nên AC căt EF tạitrung điểm củamỗi đường(1)
Ta có: EGFH là hình bình hành
nên FE cắt GH tại trug điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
nên CA cắt BD tại trug điểm của mỗi đường(3)
Từ (1), (2) và (3) suy ra AC,BF,EF,GH đồng quy
Quảng cáo
Câu hỏi hot cùng chủ đề
-
102272
-
Hỏi từ APP VIETJACK54677
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức MH2=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
43453












