Bài 4 trang 14 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:

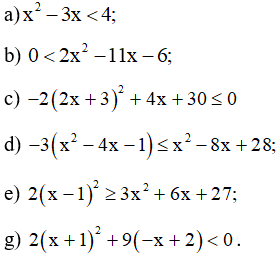
Lời giải:

a) Ta có: $x^2-3x<4$ ⟺ x² – 3x – 4 < 0

Xét tam thức bậc hai f(x) = x² – 3x – 4 có ∆ = (– 3)² – 4.1.(– 4) = 25 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 4 và x₂ = –1.

Ta có: a = 1 > 0 nên f ( x ) < 0 với –1 < x < 4.

Suy ra x² – 3x – 4 < 0 hay $x^2-3x<4$ với –1 < x < 4.

Vậy bất phương trình đã cho có tập nghiệm khi S = (–1 ; 4).

b) Ta có: 0 < 2x² – 11x – 6 ⇔ 2x² – 11x – 6 > 0

Tam thức bậc hai f( x ) = 2x² – 11x – 6 có ∆ = (– 11)² – 4.2.(– 6) = 169 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 6 và x₂ = $\frac{-1}{2}$,

Ta lại có: a = 2 > 0 nên f ( x ) > 0 khi x < $\frac{-1}{2}$ hoặc x > 6.

Vậy tập nghiệm của bất phương trình là: S =  (– ∞; $\frac{-1}{2}$) ∪ (6; +∞).

c) $-2{\left(2x+3\right)}^2+4x+30\le 0$ 

⟺ –2.( 4x² + 12x + 9 ) + 4x + 30 ≤ 0

⟺ –8x² – 24x – 18 + 4x + 30 ≤ 0

⟺ –8x² – 20x + 12 ≤ 0

⟺ –2x² – 5x + 3 ≤ 0

Tam thức bậc hai f ( x ) = –2x² – 5x + 3 có ∆ = (– 5)² – 4.(– 2).3 = 49 nên f(x) có hai nghiệm phân biệt x₁ = –3 và x₂ = $\frac{1}{2}$,

Ta lại có a = –2 < 0 nên f ( x ) ≤ 0 khi x ≤ –3 hoặc x ≥ $\frac{1}{2}$

Vậy bất phương trình đã cho có tập nghiệm là S = (–∞ ; –3] ∪ [$\frac{1}{2}$; +∞).

d) $-3\left(x^2-4x-1\right)\le x^2-8x+28$

⟺ –4x² + 20x – 25 ≤ 0

Tam thức bậc hai f ( x ) = –4x² + 20x – 25 có ∆ = 20² – 4. ( –4 ) . ( – 25 ) = 0 ,

a = –4 < 0 nên f ( x ) ≤  0 với mọi x ∈ ℝ.

Suy ra –4x² + 20x – 25 ≤ 0 với mọi x ∈ ℝ.

Vậy $-3\left(x^2-4x-1\right)\le x^2-8x+28$ với mọi x ∈ ℝ.

e) $2{\left(x-1\right)}^2\ge 3x^2+6x+27$

⟺ 2x² – 4x + 2 ≥ 3x²  + 6x + 27

⟺ –x² – 10x – 25 ≥ 0

⟺ –( x + 5 )² ≥ 0

⟺ x = –5 ( do –( x + 5 )² ≤ 0 với mọi x ∈ ℝ)

Vậy $2{\left(x-1\right)}^2\ge 3x^2+6x+27$ khi x = –5

g) $2{\left(x+1\right)}^2+9\left(-x+2\right)<0$

⇔ 2(x² + 2x + 1) – 9x + 18 < 0

⇔ 2x² – 5x + 20 < 0

Tam thức bậc hai f ( x ) = 2x² – 5x + 20 có ∆ = (– 5)² – 4. 2 . 20 = –135 < 0,

Ta lại có a = 2 > 0 nên f ( x ) > 0 với mọi x ∈ ℝ.

Suy ra 2x² – 5x + 20 > 0 với mọi x ∈ ℝ.

Vậy không tồn tại x thỏa mãn $2{\left(x+1\right)}^2+9\left(-x+2\right)<0$.