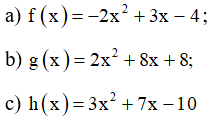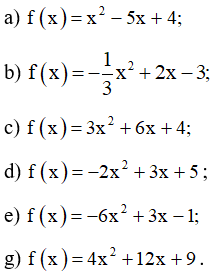Giải SBT Toán 10 trang 8 Tập 2

Bài 1 trang 8 SBT Toán 10 Tập 2: Tính biệt thức và nghiệm (nếu có) của các tam thức bậc hai sau. Xác định dấu của chúng tại x = -2.

Lời giải:

a) Ta có:  ∆ = b² – 4ac = 3² – 4.( –2).( –4) = –23 < 0 nên f(x) vô nghiệm và f (x) cùng dấu với a với mọi giá trị x.

Ta lại có: a = 0 – 2 < 0 nên tại x = – 2 thì f(– 2) < 0.

Vì vậy f(x) âm tại x = –2.

b) Ta có: ∆ = b² – 4ac = 8² – 4.2.8 = 0 nên g (x) = 0 có nghiệm kép là:

x₀ = $\frac{-\text{b}}{2\text{a}}$ = $\frac{-8}{2.2}$ = – 2. Do đó g (– 2) = 0.

Vì vậy g(x) không âm cũng không dương tại x = –2.

c) Ta có: ∆ = b² – 4ac = 7² – 4.3.( – 10 ) = 169 > 0 nên h(x) có hai nghiệm phân biệt lần lượt là:

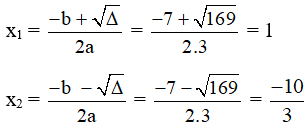
h(– 2) = 3.(– 2)² + 7.(– 2) – 10 = – 12 < 0.

Vì vậy h(x) âm tại x = – 2.

Giải SBT Toán 10 trang 9 Tập 2

Bài 2 trang 9 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:

a) $f\left(x\right)=\left(2m-8\right)x^2+2mx+1$ là một tam thức bậc hai;

b) $f\left(x\right)=\left(2m+3\right)x^2+3x-4m^2$ là một tam thức bậc hai có x = 3 là một 

c) $f\left(x\right)=2x^2+mx-3$ nghiệm;dương tại x = 2.

Lời giải:

a) $f\left(x\right)$ là tam thức bậc hai khi và chỉ khi 2m – 8 ≠ 0 hay m ≠ 4.

b) $f\left(x\right)$ là tam thức bậc hai khi và chỉ khi 2m + 3 ≠ 0 hay m ≠ $\frac{-3}{2}$.

Tam thức $f\left(x\right)$ có x = 3 là một nghiệm khi và chỉ khi f (3) = (2m + 3) . 3² + 3.3 – 4m² = 0

Suy ra – 4m² + 18m + 36 = 0 hay – 2m² + 9m + 18 = 0

Ta có: ∆ = b² – 4ac = 9² – 4.( –2 ).18 = 225 > 0 nên phương trình ẩn m có hai nghiệm phân biệt lần lượt là:

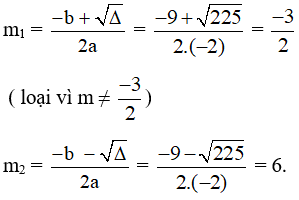
Vậy m = 6 thỏa mãn f(x) là tam thức bậc hai có x = 3 là một nghiệm.

c) $f\left(x\right)=2x^2+mx-3$ dương tại x = 2 khi và chỉ khi f (2) = 2.2² + 2m – 3 > 0

Suy ra 2m + 5 > 0 ⟺ m > $\frac{-5}{2}$.

Vậy m > $\frac{-5}{2}$ thì f(x) dương tại x = 2.

Bài 3 trang 9 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:

a) $f\left(x\right)=\left(m^2+9\right)x^2+\left(m+6\right)x+1$ là một tam thức bậc hai có một nghiệm duy nhất;

b) $f\left(x\right)=\left(m-1\right)x^2+3x+1$ là một tam thức bậc hai có hai nghiệm phân biệt;

c) $f\left(x\right)=m{x}^2+\left(m+2\right)x+1$ là một tam thức bậc hai vô nghiệm.

Lời giải:

a) $f\left(x\right)$ là một tam thức bậc hai khi và chỉ khi m² + 9 ≠ 0, mà m² + 9 > 0, đúng với mọi m ∈ R.

$f\left(x\right)$ có một nghiệm duy nhất khi ∆ = b² – 4ac = (m + 6)² – 4.(m² + 9).1 = 0

⇔ –3m² + 12m = 0

⇔ 3m.(4 – m) = 0

⇔ m = 0 hoặc m = 4

Vậy m = 0 hoặc m = 4 là một tam thức bậc hai có một nghiệm duy nhất.

b) $f\left(x\right)$ là một tam thức bậc hai khi và chỉ khi m – 1 ≠ 0 hay m ≠ 1.

$f\left(x\right)$ có hai nghiệm phân biệt khi và chỉ khi ∆ = b² – 4ac = 3² – 4. (m – 1 ).1 > 0

⇔ 13 – 4m > 0

⇔ m < $\frac{13}{4}$.

Vậy m < $\frac{13}{4}$ thì f(x) là một tam thức bậc hai có hai nghiệm phân biệt.

c) f(x) là một tam thức bậc hai khi a = m ≠ 0.

Ta có: ∆ = (m + 2)² – 4m = m² + 4 > 0

Để f(x) vô nghiệm thì ∆ < 0 ⇔ m² + 4 < 0

Mà m² + 4 > 0 với mọi m nên không tồn tại giá trị của m thỏa mãn.

Vậy không có giá trị nào của m thỏa mãn yêu cầu.

Bài 4 trang 9 SBT Toán 10 Tập 2: Dựa vào đồ thị của các hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai tương ứng:

Lời giải:

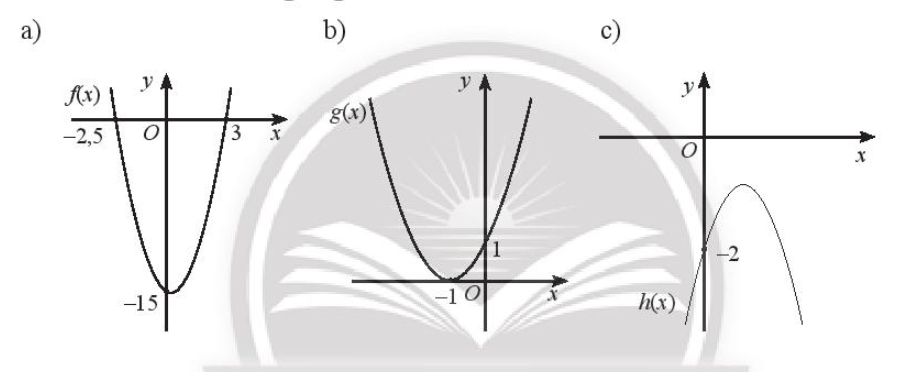
a) Quan sát hình vẽ a), ta thấy:

Đồ thị hàm số nằm trên trục hoành khi x < – 2,5 hoặc x > 3 hay f(x) > 0 khi x ∈ ( – ∞; – 2,5) ∪ (3; + ∞).

Đồ thị cắt trục hoành tại hai điểm x = – 2,5 và x = 3 hay f(x) = 0 khi x = – 2,5 và x = 3.

Đồ thị hàm số nằm dưới trục hoành khi – 2,5 < x < 3 hay f(x) < 0 khi x ∈ (– 2,5; 3).

b) Quan sát hình vẽ b) ta thấy:

Đồ thị hàm số nằm trên trục hoành khi x ≠ –1 hay g(x) > 0 khi x ≠ –1.

Đồ thị cắt trục hoành tại điểm x =  –1 hay fgx) = 0 khi x = – 1.

c) Đồ thị hàm số nằm dưới trục hoành với mọi x ∈ ℝ hay f(x) < 0 với mọi x ∈ ℝ.

Bài 5 trang 9 SBT Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau:

Lời giải:

a) Ta có: ∆ = b² – 4ac = (– 5)² – 4.1.4 = 9 > 0 nên f (x) có hai nghiệm phân biệt lần lượt là:

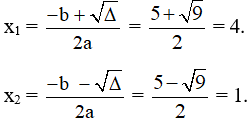
Như vậy, f (x) có a = 1 > 0, ∆ > 0 và có hai nghiệm x₁ = 1, x₂ = 4 nên áp dụng định lí dấu tam thức bậc hai, ta có:

f (x) âm trong khoảng (1;  4).

f (x) dương trong khoảng (–∞; 1) và (4; +∞).

b) Ta có: ∆ = b² – 4ac = 2² – 4.$\left(\frac{-1}{3}\right)$.( –3) = 0 nên f (x) có nghiệm kép x₀ = $\frac{-b}{2a}$ = 3.

Như vậy, f (x) có a = $\frac{-1}{3}$ < 0, ∆ = 0 nên f (x) âm với mọi x ≠ 3.

c) Ta có: ∆ = b² – 4ac = 6² – 4.3.4 = –12 < 0, a = 3 > 0 nên f (x) dương với mọi x ∈ ℝ.

d) Ta có: ∆ = b² – 4ac = 3² – 4.(–2).5 = 49 > 0 nên f (x) có hai nghiệm phân biệt lần lượt là:

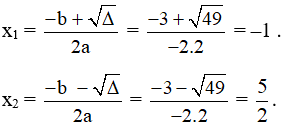
Như vậy, f (x) có a = –2  < 0, ∆ > 0 và có hai nghiệm x₁ = –1, x₂ = $\frac{5}{2}$ nên:

f (x) dương trong khoảng ( –1; $\frac{5}{2}$).

f (x) âm trong khoảng (–$\frac{5}{2}$; –1) và ($\frac{5}{2}$; +$\infty$).

e) Ta có: ∆ = b² – 4ac = 3² – 4.( –6 ) .( –1 ) = –15 < 0, a = –6  < 0 nên f ( x ) âm với mọi x ∈ ℝ.

g) Ta có: ∆ = b² – 4ac = 12² – 4.4.9 = 0 nên f (x) có nghiệm kép $\frac{-3}{2}$

Như vậy, f (x) có a = 4 > 0, ∆ = 0 nên f (x) dương với mọi x ≠ $\frac{-3}{2}$.

Bài 6 trang 9 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:

a) $f\left(x\right)=\left(m+1\right)x^2+5x+2$ là tam thức bậc hai không đổi dấu trên ℝ,

b) $f\left(x\right)=m{x}^2-7x+4$ là tam thức bậc hai âm với mọi x ∈ ℝ;

c) $f\left(x\right)=3x^2-4x+\left(3m-1\right)$ là tam thức bậc hai dương với mọi x ∈ ℝ;

d) $f\left(x\right)=\left(m^2+1\right)x^2-3mx+1$ là tam thức bậc hai âm với mọi x ∈ ℝ.

Lời giải:

a) f (x) là tam thức bậc hai khi và chỉ khi m + 1 ≠ 0 hay m ≠  –1

f (x) không đổi dấu trên ℝ khi và chỉ khi ∆ = b² – 4ac = 5² – 4.( m + 1 ). 2 < 0

⇔ 17 – 8m < 0

⇔ m > $\frac{17}{8}$.

Vậy m > $\frac{17}{8}$ thỏa mãn yêu cầu đề bài.

b) f (x) là tam thức bậc hai âm với mọi x ∈ ℝ khi và chỉ khi m < 0 và

∆ = b² – 4ac = 49 – 16m < 0 ⇔ m > $\frac{49}{16}$ 

Do đó m thỏa mãn đồng thời m < 0 và m > $\frac{49}{16}$ (vô lí).

Vậy không tồn tại m thỏa mãn yêu cầu đề bài.

c) Do f (x) có a = 3 > 0 nên f (x) là tam thức bậc hai dương với mọi x ∈ ℝ khi và chỉ khi ∆’ = 4 – 3.(3m – 1 ) < 0

⇔ 7 – 9m < 0

⇔ m > $\frac{7}{9}$

Vậy m > $\frac{7}{9}$ thoả mãn yêu cầu đề bài.

d) f (x) là tam thức bậc hai âm với mọi x ∈ ℝ khi và chỉ khi a = m² + 1 < 0 và ∆ < 0.

Ta có m² ≥ 0 với mọi x ∈ ℝ 

⇒ a = m² + 1 > 0 với mọi x ∈ ℝ.

Như vậy không tồn tại m thỏa mãn yêu cầu đề bài.

Giải SBT Toán 10 trang 10 Tập 2

Bài 7 trang 10 SBT Toán 10 Tập 2: Chứng minh rằng:

a) $2x^2+\sqrt{3}x+1>0$ với mọi x ∈ ℝ;

b) $x^2+x+\frac{1}{4}\ge 0$với mọi x ∈ ℝ,

c) $-x^2<-2x+3$ với mọi x ∈ ℝ.

Lời giải:

a) Tam thức bậc hai $2x^2+\sqrt{3}x+1$ có a = 2 > 0, ∆ = 3 – 4.2.1 = –5 < 0 với mọi x ∈ ℝ. Như vậy $2x^2+\sqrt{3}x+1>0$ với mọi x ∈ ℝ.

b) Tam thức bậc hai $x^2+x+\frac{1}{4}$ có a = 1 > 0, ∆ = 1 – 4.1.$\frac{1}{4}$ = 0 nên $x^2+x+\frac{1}{4}\ge 0$ với mọi x ∈ ℝ.

c) Tam thức bậc hai –x² + 2x – 3 có a = –1 < 0, ∆ = 4 – 4.( –1).( –3) = –8 < 0 với mọi x ∈ ℝ. Như vậy –x² + 2x – 3 < 0 với mọi x ∈ ℝ hay $-x^2<-2x+3$ với mọi x ∈ ℝ.

Bài 8 trang 10 SBT Toán 10 Tập 2:Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai $f\left(x\right)=x^2+bx+c$ trong mỗi trường hợp sau:

a) Đồ thị của hàm số $f\left(x\right)$ đi qua ba điểm có toạ độ là (– 1; – 4), (0; 3) và (1; –14);

b) Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0; –2), (2; 6) và (3; 13);

c) f(– 5) = 33, f (0) = 3 và f(2) = l9.

Lời giải:

a) Theo đề bài:

Đồ thị của hàm số $y=f\left(x\right)$ đi qua điểm có toạ độ là (– 1; – 4) nên –4 = a – b + c (1)

Đồ thị của hàm số $y=f\left(x\right)$ đi qua điểm có toạ độ là (0; 3) nên 3 = c (2)

Đồ thị của hàm số y = f(x) đi qua điểm có toạ độ là (1; – 14) nên –14 = a + b + c (3)

Thay (2) vào phương trình (1) và (3) ta có:

$$\begin{gathered} \left\{\begin{array}{l}\text{a}-\text{b}=-7\\ \text{a}+\text{b}=-17\end{array}\right.\iff \left\{\begin{array}{l}2a=-24\\ \text{a}+\text{b}=-17\end{array}\right. \\ \iff \left\{\begin{array}{l}a=-12\\ -12+\text{b}=-17\end{array}\right.\iff \left\{\begin{array}{l}a=-12\\ \text{b}=-5\end{array}\right. \end{gathered}$$ 

Vậy f (x) = –12x² – 5x + 3.

Xét f ( x ) = –12x² – 5x + 3 có ∆ = (– 5)² – 4.(–12).3 = 169 > 0 nên f (x) có hai nghiệm phân biệt lần lượt là:

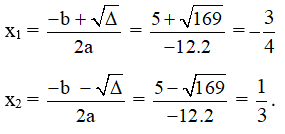
Như vậy, f (x) có a = –12 < 0, ∆ > 0 và có hai nghiệm x₁ = –$\frac{3}{4}$, x₂ = $\frac{1}{3}$  nên:

f (x) dương trong khoảng ( –$\frac{3}{4}$; $\frac{1}{3}$ ).

f (x) âm trong khoảng $\left(-\infty ;\frac{-3}{4}\right)$ và $\left(\frac{1}{3};+\infty \right)$

b) Ta có:

Đồ thị của hàm số $y=f\left(x\right)$ đi qua điểm có toạ độ là (0; – 2) nên –2 = c (1)

Đồ thị của hàm số $y=f\left(x\right)$ đi qua ba điểm có toạ độ là (2; 6) nên 6 = 4a + 2b + c (2)

Đồ thị của hàm số $y=f\left(x\right)$ đi qua ba điểm có toạ độ là (3; 13) nên 13 = 9a + 3b + c (3).

Thay (1) vào phương trình (2) và (3) ta có:

$$\begin{gathered} \left\{\begin{array}{l}\text{4a + }2\text{b}=8\\ \text{9a}+3\text{b}=15\end{array}\right.\iff \left\{\begin{array}{l}\text{2a + b}=4\\ \text{3a}+\text{b}=5\end{array}\right. \\ \iff \left\{\begin{array}{l}\text{a }=1\\ \text{3.1}+\text{b}=5\end{array}\right.\iff \left\{\begin{array}{l}\text{a }=1\\ \text{b}=2\end{array}\right. \end{gathered}$$ 

Do đó f (x) = x² + 2x – 2.

Xét f ( x ) = x² + 2x – 2 có ∆ = 2² – 4.( –2 ).1 = 12 nên f ( x ) có hai nghiệm phân biệt lần lượt là:

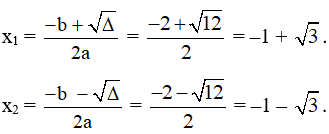
Như vậy, f (x) có a = 1 > 0, ∆ > 0 và có hai nghiệm x₁ = –1 + $\sqrt{3}$, x₂ = –1 – $\sqrt{3}$ nên:

f (x) âm trong khoảng ( –1 – $\sqrt{3}$; –1 + $\sqrt{3}$ ).

f (x) dương trong khoảng 

c) Ta có:

f(– 5) = 33 nên 33 = 25a – 5b + c (1)

f (0) = 3 nên 3 = c (2)

f(2) = 19 nên 19 = 4a + 2b + c (3)

Thay (2) vào phương trình (1) và (3) ta có $\left\{\begin{array}{l}25a-5b=30\\ \text{4a}+2\text{b}=16\end{array}\right.$ . Giải hệ phương trình ta được a = 2 và b =  4.

Vậy f (x) = 2x² + 4x + 3.

Xét f (x) = 2x² + 4x +3 có ∆ = 4² – 4.2.3 = –8 < 0, a = 2 > 0 nên f (x) dương với mọi x ∈ ℝ.