Giải các bất phương trình bậc hai sau

Lời giải Bài 3 trang 14 SBT Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

417
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 10 Chân trời sáng tạo Bài 2: Giải bất phương trình bậc hai một ẩn

Bài 3 trang 14 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:

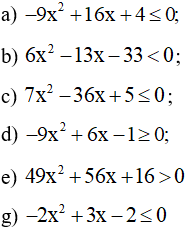
Sách bài tập Toán 10 Bài 2: Giải bất phương trình bậc hai một ẩn - Chân trời sáng tạo (ảnh 1)

 

Lời giải:

a) Tam thức bậc hai f (x) = –9x2 + 16x + 4 có a = – 9 < 0 và ∆ = 162 – 4.( – 9).4 = 112 > 0. Do đó f(x) có hai nghiệm phân biệt là x1 = 2 và x2 = −29

Áp dụng định lí về dấu tam thức bậc hai ta có:

−9x2+16x+4≤0 khi x ≤ -29 hoặc x ≥ 2.

Vậy tập nghiệm của bất phương trình là S = −∞;−29∪2;+∞.

b) Tam thức bậc hai f (x) = 6x2−13x−33 có a = 6 > 0 và ∆ = ( –13)2 – 4.6.( –33) = 961 > 0. Do đó f(x) có hai nghiệm phân biệt là x1 = 113 và x2 = -32

Áp dụng định lí về dấu tam thức bậc hai ta có:

6x2−13x−33 < 0 khi −32 < x < 113

Vậy tập nghiệm của bất phương trình là S = −32;113.

c) Tam thức bậc hai f ( x ) = 7x2−36x+5 có a = 7 > 0 và 2∆ = ( –36)2 – 4.7.5 = 1156 > 0. Do đó f(x) có hai nghiệm phân biệt là x1 = 17 và x2 = 5

Áp dụng định lí về dấu tam thức bậc hai ta có:

7x2−36x+5≤0  khi 17 ≤ x ≤ 5

Vậy tập nghiệm của bất phương trình là S = 17;5.

d) Tam thức bậc hai f ( x ) = −9x2+6x−1 có a = –9 < 0 và ∆ = 62 – 4.( –9).( –1) = 0. Do đó f(x) có nghiệm x = 13

Áp dụng định lí về dấu tam thức bậc hai ta có:

−9x2+6x−1≥0 khi x = 13

Vậy tập nghiệm của bất phương trình là S = 13.

e) Tam thức bậc hai f ( x ) = 49x2+56x+16 = ( 7x + 4 )2

Tam thức bậc hai có nghiệm x = -47

Áp dụng định lí về dấu tam thức bậc hai ta có:

49x2+56x+16>0  khi x ≠ -47

Vậy tập nghiệm của bất phương trình là S = ℝ\−47

g)

Tam thức bậc hai f ( x ) = −2x2+3x−2 có ∆ = 32 – 4. ( –2 ). ( –2 ) = –7 < 0 nên f(x) vô nghiệm.

Áp dụng định lí về dấu tam thức bậc hai ta có a = –2 < 0 nên

−2x2+3x−2≤0 với mọi x ∈ ℝ.

Vậy −2x2+3x−2≤0 với mọi x ∈ ℝ.

Xem thêm các bài giải sách bài tập Toán 10 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1 trang 13 SBT Toán 10 Tập 2: x = 2 là một nghiệm của bất phương trình nào sau đây?...

Bài 2 trang 13 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng...

Bài 3 trang 14 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau...

Bài 4 trang 14 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau...

Bài 5 trang 14 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau...

Bài 6 trang 14 SBT Toán 10 Tập 2: Tìm giá trị của tham số m để: a) x = 3 là một nghiệm của bất phương trình m2−1x2+2mx−15≤0...

Bài 7 trang 14 SBT Toán 10 Tập 2: Với giá trị nào của tham số m thì: a) Phương trình 4x2+2m−2x+m2=0 có nghiệm...

Bài 8 trang 14 SBT Toán 10 Tập 2: Lợi nhuận thu được từ việc sản xuất và bán x sản phẩm thủ công của một cửa hàng là...

Bài 9 trang 15 SBT Toán 10 Tập 2: Một quả bóng được ném thẳng lên từ độ cao h0 (m) với vận tốc v0(m/s). Độ cao của bóng so với mặt đất (tính bằng mét) sau t (s) được cho bởi hàm số...

Bài 10 trang 15 SBT Toán 10 Tập 2: Từ độ cao y0 mét, một quả bóng được ném lên xiên một góc α so với phương ngang với vận tốc đầu v0 có phương trình chuyển động...

Bài 11 trang 15 SBT Toán 10 Tập 2: Một hình chữ nhật có chu vi bằng 20 cm. Để điện tích hình chữ nhật lớn hơn hoặc bằng 15 cm2 thì chiều rộng của hình chữ nhật nằm trong khoảng bao nhiêu?...

Bài 12 trang 15 SBT Toán 10 Tập 2: Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m...

417
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm