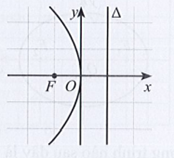Giải SBT Toán 10 trang 95 Tập 2

Bài 59 trang 95 SBT Toán 10 Tập 2: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\left(a>b>0\right)$ ?

A.

B.

C.

D.

Lời giải:

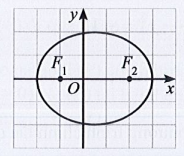
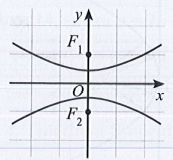
Ta thấy phương trình chính tắc:  $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Khi cho x = 0 ta được y = ±b

Khi cho y = 0 ta được x = ±a

Do đó suy ra Elip đối xứng qua trục Ox và Oy và có tiêu điểm F₁, F₂ nằm trên trục Ox.

Vậy chọn đáp án C.

Bài 60 trang 95 SBT Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của elip?

A. $\frac{x^2}{3^2}+\frac{y^2}{3^2}=1$ ;

B. $\frac{x^2}{3^2}-\frac{y^2}{3^2}=1$ ;

C. $\frac{x^2}{6}+y^2=1$ ;

D. $\frac{x^2}{2^2}+\frac{y^2}{3^2}=1$ .

Lời giải:

Ta thấy phương trình chính tắc của Elip có dạng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0)

Vậy chọn đáp án C.

Giải SBT Toán 10 trang 96 Tập 2

Bài 61 trang 96 SBT Toán 10 Tập 2: Hypebol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\left(a>\mathrm{0,}b>0\right)$ ?

A.

B.

C.

D.

Lời giải:

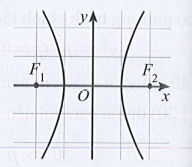
Hypebol có dạng phương trình chính tắc $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\left(a>\mathrm{0,}b>0\right)$ là

Thì có tiêu điểm nằm trên trục Ox.

Cho y = 0 ta được x = ±a

Do đó Hypebol này đối xứng qua trục Oy.

Vậy ta chọn đáp án B.

Bài 62 trang 96 SBT Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của hypebol?

A. $x^2+\frac{y^2}{3^2}=1$ ;

B. $\frac{x^2}{16}-y^2=-1$ ;

C. $\frac{x^2}{25}-\frac{y^2}{9}=-1$ ;

D. $x^2-\frac{y^2}{2}=1$ .

Lời giải:

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\left(a>\mathrm{0,}b>0\right)$ là phương trình chính tắc của Hypebol.

Do đó chỉ có phương trình ở ý D là thỏa mãn.

Vậy ta chọn đáp án D.

Bài 63 trang 96 SBT Toán 10 Tập 2: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: y² = 2px (p > 0)

A.

B.

C.

D.

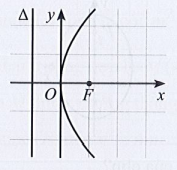
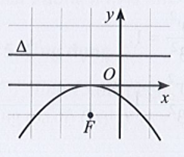
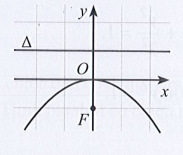
Lời giải:

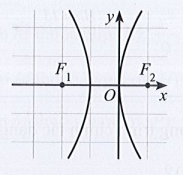
Parabol có dạng y² = 2px (p > 0).

Ta thấy Parabol đối xứng qua trục Ox.

Do p > 0 nên x ≥ 0 thì hàm số có nghĩa, do đó đồ thị nằm bên phải trục Oy.

Vậy chọn đáp án A.

Giải SBT Toán 10 trang 97 Tập 2

Bài 64 trang 97 SBT Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của parabol?

A. $y^2=-\mathrm{0,3}x$ ;
B. $x^2=\mathrm{0,3}y$ ;

C. $y^2=\mathrm{0,3}x$ ;

D. $x^2=-\mathrm{0,3}y$ .

Lời giải:

Phương trình chính tắc của parabol có dạng là: (p >0)

Do đó ta thấy phương trình $y^2=\mathrm{0,3}x$  là đúng dạng này.

Vậy chọn đáp án C.

Bài 65 trang 97 SBT Toán 10 Tập 2: Lập phương trình chính tắc của elip (E) biết (E) đi qua hai điểm $P\left(2;\frac{3\sqrt{3}}{2}\right)$  và  $Q\left(2\sqrt{2};\frac{3\sqrt{2}}{2}\right)$

Lời giải:

(E) có phương trình chính tắc là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$  (a > b > 0).

Do P thuộc (E) nên ta có:

$\frac{2^2}{a^2}+\frac{{\left(\frac{3\sqrt{3}}{2}\right)}^2}{b^2}=1\iff \frac{4}{a^2}+\frac{27}{4b^2}=1$                   (1)

Do Q thuộc (E) nên ta có:

$\frac{{\left(2\sqrt{2}\right)}^2}{a^2}+\frac{{\left(\frac{3\sqrt{2}}{2}\right)}^2}{b^2}=1\iff \frac{8}{a^2}+\frac{9}{2b^2}=1$                   (2)

Từ (1) và (2) ta có  hệ phương trình hai ẩn :$\frac{1}{a^2},\frac{1}{b^2}$

Coi  là 2 ẩn của hệ phương trình

Suy ra    $\frac{1}{a^2}=\frac{1}{16};\frac{1}{b^2}=\frac{1}{9}\Rightarrow a^2=\mathrm{16,}{b}^2=9$

Phương trình chính tắc của (E): $\frac{x^2}{16}+\frac{y^2}{9}=1$  .

Bài 66 trang 97 SBT Toán 10 Tập 2: Cho elip $\left(E\right):\frac{x^2}{9}+\frac{y^2}{4}=1$ . Tìm điểm P thuộc (E) thỏa mãn OP = 2,5.

Lời giải:

Gọi điểm P có tọa độ P(m; n).

Do OP = 2,5 nên  $m^2+n^2=\frac{25}{4}$

Do P thuộc (E) nên ta có:  $\frac{1}{9}{m}^2+\frac{1}{4}{n}^2=1$

Suy ra ta có hệ phương trình $\left\{\begin{array}{l}{m}^2+n^2=\frac{25}{4}\\ \frac{1}{9}{m}^2+\frac{1}{4}{n}^2=1\end{array}\right.\iff \left\{\begin{array}{l}{m}^2=\frac{81}{20}\\ n^2=\frac{11}{5}\end{array}\right.$

Suy ra  $m^2=\frac{81}{20};n^2=\frac{11}{5}\Rightarrow m=\pm \frac{9\sqrt{5}}{10};n=\pm \frac{\sqrt{55}}{5}$ .

Vậy có 4 tọa độ của điểm P:

$\left(\frac{9\sqrt{5}}{10};\frac{\sqrt{55}}{5}\right);\left(\frac{9\sqrt{5}}{10};\frac{-\sqrt{55}}{5}\right);\left(\frac{-9\sqrt{5}}{10};\frac{\sqrt{55}}{5}\right);\left(\frac{-9\sqrt{5}}{10};\frac{-\sqrt{55}}{5}\right)$.

Bài 67 trang 97 SBT Toán 10 Tập 2: Lập phương trình chính tắc của hypebol (H), biết (H) đi qua hai điểm M(- 1; 0) và $N\left(2;2\sqrt{3}\right)$ .

Lời giải:

Hypebol có phương trình chính tắc là:  $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\left(a>\mathrm{0,}b>0\right)$

Do M(-1; 0) thuộc (H) nên ta có:  $\frac{{\left(-1\right)}^2}{a^2}-\frac{0^2}{b^2}=1\Rightarrow a^2=1$

Do N(2; ) thuộc (H) nên ta có:  $\frac{2^2}{1}-\frac{{\left(2\sqrt{3}\right)}^2}{b^2}=1\Rightarrow b^2=4$

Suy ra phương trình chính tắc của Hypebol là: $\frac{2^2}{1}-\frac{{\left(2\sqrt{3}\right)}^2}{b^2}=1\Rightarrow b^2=4$ .

Bài 68 trang 97 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình chính tắc: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$  với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.

Lời giải:

Thay y = n vào phương trình chính tắc của Parabol ta có:  $\frac{x^2}{a^2}-\frac{n^2}{b^2}=1$

Suy ra  $x^2=a^2.\left(1+\frac{n^2}{b^2}\right)$

 $\Rightarrow \left[\begin{array}{l}x=a\sqrt{\left(1+\frac{n^2}{b^2}\right)}\\ x=-a\sqrt{\left(1+\frac{n^2}{b^2}\right)}\end{array}\right.$

Giả sử điểm P $\left(a\sqrt{\left(1+\frac{n^2}{b^2}\right)};n\right)$ và Q  $\left(-a\sqrt{\left(1+\frac{n^2}{b^2}\right)};n\right)$

Do Q và P có cùng tung độ và hoành độ đối nhau nên P và Q đối xứng nhau qua trục Oy

Bài 69 trang 97 SBT Toán 10 Tập 2: Viết phương trình chính tắc của parabol (P) biết:

a) Phương trình đường chuẩn của (P) là: $x+\frac{1}{8}=0$ .

b) (P) đi qua điểm M(1; - 8).

Lời giải:

a) Gọi phương trình chính tắc của Parabol là:  $y^2=2px\left(p>0\right)$

Phương trình đường chuẩn của (P) là x $+\frac{1}{8}$  = 0 nên  $\frac{p}{2}=\frac{1}{8}$

Suy ra p =  $\frac{1}{4}$

Vậy phương trình chính tắc của (P) là: $y^2=\frac{1}{2}x$ .

b) Gọi phương trình chính tắc của Parabol là:  $y^2=2px\left(p>0\right)$

Do (P) đi qua điểm M(1; -8). Thay tọa độ điểm M vào phương trình chính tắc ta có:

 ${\left(-8\right)}^2=2p.1\Rightarrow p=32$

Vậy phương trình chính tắc của (P) là: $y^2=64x$ .

Bài 70 trang 97 SBT Toán 10 Tập 2: Cho parabol (P) có phương trình chính tắc: y² = 2px (p > 0) và đường thẳng x = m (m > 0) cắt (P) tại hai điểm I, K phân biệt. Chứng minh hai điểm I và K đối xứng nhau qua trục Ox.

Lời giải:

Thay x = m vào phương trình chính tắc của Parabol ta có:

  $y^2=2pm$$\Rightarrow \left[\begin{array}{l}y=\sqrt{2pm}\\ y=-\sqrt{2pm}\end{array}\right.$ 

Ta giả sử điểm I $\left(m;\sqrt{2pm}\right)$ và điểm K  $\left(m;-\sqrt{2pm}\right)$

Do I và K có cùng hoành độ và tung độ đối nhau nên I và K đối xứng nhau qua trục Ox.