Giải SBT Toán 10 trang 61 Tập 2

Bài 1 trang 61 SBT Toán 10 Tập 2: Tọa độ của vectơ $\overrightarrow{u}=-3\overrightarrow{i}+2\overrightarrow{j}$là:

A. (- 3; 2);

B. (2; - 3);

C. $\left(-3\overrightarrow{i};2\overrightarrow{j}\right)$ ;

D. (3; 2).

Lời giải:

Do $\overrightarrow{u}=-3\overrightarrow{i}+2\overrightarrow{j}$  mà $\overrightarrow{i},\overrightarrow{j}$  là các vectơ đơn vị tương ứng với trục Ox và Oy

Nên $\overrightarrow{u}=\left(-3;2\right)$ .

Vậy chọn đáp án A.

Bài 2 trang 61 SBT Toán 10 Tập 2: Tọa độ của vectơ $\overrightarrow{u}=5\overrightarrow{j}$  là:

A. (5; 0);

B. $\left(5;\overrightarrow{j}\right)$ ;

C. $\left(0;5\overrightarrow{j}\right)$ ;

D. (0; 5).

Lời giải:

Do $\overrightarrow{u}=5\overrightarrow{j}$  mà $\overrightarrow{i},\overrightarrow{j}$  là các vectơ đơn vị tương ứng với trục Ox và Oy

Nên $\overrightarrow{u}=\left(0;5\right)$ .

Vậy chọn đáp án D.

Bài 3 trang 61 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(2; - 5). Tọa độ của vectơ $\overrightarrow{OA}$  là:

A. (2; 5);

B. (2; - 5);

C. (- 2; - 5);

D. (- 2; 5).

Lời giải:

Tọa độ của vectơ $\overrightarrow{OA}$  chính là tọa độ điểm A và là: $\overrightarrow{OA}=\left(2;-5\right)$ .

Vậy chọn đáp án B.

Bài 4 trang 61 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(- 1; 3), B(2; - 1). Tọa độ của vectơ $\overrightarrow{AB}$  là:

A. (1; - 4);

B. (- 3; 4);

C. (3; - 4);

D. (1; - 2).

Lời giải:

Tọa độ của vectơ $\overrightarrow{AB}$  là hiệu số tọa độ tương ứng của điểm B và điểm A.

Do đó: $\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(2+1;-1-3\right)=\left(3;-4\right)$ .

Vậy chọn đáp án C.

Bài 5 trang 61 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{u}=\left(-2;-4\right),\overrightarrow{v}=\left(2x-y;y\right)$ . Hai vectơ $\overrightarrow{u}$  và $\overrightarrow{v}$  bằng nhau nếu:

A. $\left\{\begin{array}{c}x=1\\ y=-4\end{array}\right.$ ;

B. $\left\{\begin{array}{c}x=-3\\ y=-4\end{array}\right.$ ;

C. $\left\{\begin{array}{c}x=1\\ y=4\end{array}\right.$ ;

D. $\left\{\begin{array}{c}x=-3\\ y=4\end{array}\right.$ .

Lời giải:

Hai vectơ $\overrightarrow{u}$  và $\overrightarrow{v}$  bằng nhau nếu tọa độ tương ứng của chúng bằng nhau

Hay  $\left\{\begin{array}{l}2x-y=-2\\ y=-4\end{array}\right.\iff \left\{\begin{array}{l}2x-\left(-4\right)=-2\\ y=-4\end{array}\right.\iff \left\{\begin{array}{l}2x=-6\\ y=-4\end{array}\right.\iff \left\{\begin{array}{l}x=-3\\ y=-4\end{array}\right.$.

Vậy chọn đáp án B.

Bài 6 trang 61 SBT Toán 10 Tập 2: Cho hình bình hành ABCD có A(- 1; - 2), B(3; 2), C(4; - 1). Tọa độ của đỉnh D là:

A. (8; 3);

B. (3; 8);

C. (- 5; 0);

D. (0; - 5).

Lời giải:

Ta có:  $\overrightarrow{AB}=\left(3+1;2+2\right)=\left(4;4\right)$

Gọi D(a; b) thì  $\overrightarrow{DC}=\left(4-a;-1-b\right)$

Do ABCD là hình bình hành nên ta có:  $\overrightarrow{AB}=\overrightarrow{DC}$

Hay $\left\{\begin{array}{l}4-a=4\\ -1-b=4\end{array}\right.\iff \left\{\begin{array}{l}a=0\\ b=-5\end{array}\right.$ .

Suy ra D(0; -5).

Vậy chọn đáp án D.

Bài 7 trang 61 SBT Toán 10 Tập 2: Tìm tọa độ của các vectơ trong Hình 4.

Lời giải:

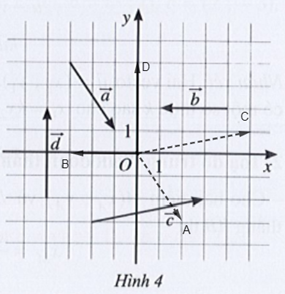
Ta vẽ vectơ $\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c},\overrightarrow{OD}=\overrightarrow{d}$ .

Quan sát trên hình vẽ, ta có:

A(2; – 3) nên $\overrightarrow{a}=\left(2;-3\right)$ ;

B(– 3; 0) nên $\overrightarrow{b}=\left(-3;0\right)$ ;

C(5; 1) nên $\overrightarrow{c}=\left(5;1\right)$ ;

D(0; 4) nên $\overrightarrow{d}=\left(0;4\right)$ .

Giải SBT Toán 10 trang 62 Tập 2

Bài 8 trang 62 SBT Toán 10 Tập 2: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:

a) $\overrightarrow{m}=\left(2a+3;b-1\right)$  và $\overrightarrow{n}=\left(1;-2\right)$ ;

b) $\overrightarrow{u}=\left(3a-2;5\right)$  và $\overrightarrow{v}=\left(5;2b+1\right)$ ;

c) $\overrightarrow{x}=\left(2a+b;2b\right)$  và $\overrightarrow{y}=\left(3+2b;b-3a\right)$ .

Lời giải:

2 vectơ bằng nhau thì tọa độ tương ứng của chúng phải bằng nhau.

a) Ta có: $\overrightarrow{m}=\left(2a+3;b-1\right)$  và $\overrightarrow{n}=\left(1;-2\right)$  bằng nhau

 $\iff \left\{\begin{array}{l}2a+3=1\\ b-1=-2\end{array}\right.\iff \left\{\begin{array}{l}2a=-2\\ b=-1\end{array}\right.\iff \left\{\begin{array}{l}a=-1\\ b=-1\end{array}\right.$

Vậy a = – 1, b = – 1.

b. Ta có: $\overrightarrow{u}=\left(3a-2;5\right)$  và $\overrightarrow{v}=\left(5;2b+1\right)$  bằng nhau

 $\iff \left\{\begin{array}{l}3a-2=5\\ 5=2b+1\end{array}\right.\iff \left\{\begin{array}{l}3a=7\\ 2b=4\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{7}{3}\\ b=2\end{array}\right.$

Vậy a = $\frac{7}{3}$  , b = 2.

c. Ta có: $\overrightarrow{x}=\left(2a+b;2b\right)$  và $\overrightarrow{y}=\left(3+2b;b-3a\right)$  bằng nhau

$\iff \left\{\begin{array}{l}2a+b=3+2b\\ 2b=b-3a\end{array}\right.\iff \left\{\begin{array}{l}2a-b=3\\ b=-3a\end{array}\right.\iff \left\{\begin{array}{l}2a-\left(-3a\right)=3\\ b=-3a\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{3}{5}\\ b=\frac{-9}{5}\end{array}\right.$

Vậy a = $\frac{3}{5}$  và $b=\frac{-9}{5}$ .

Bài 9 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(- 4; 2), B(2; 4), C(8; - 2). Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Lời giải:

Ta có:  $\overrightarrow{AB}=\left(2+4;4-2\right)=\left(6;2\right)$

Gọi D(a; b) thì  $\overrightarrow{DC}=\left(8-a;-2-b\right)$

Do ABCD là hình bình hành nên ta có:  $\overrightarrow{AB}=\overrightarrow{DC}$

Hay $\left\{\begin{array}{l}8-a=6\\ -2-b=2\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ b=-4\end{array}\right.$ .

Suy ra D(2; -4).

Vậy D(2; -4).

Bài 10 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(x_A; y_A); B(x_B; y_B); C(x_C; y_C); D(x_D; y_D). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi $x_A+x_C=x_B+x_D$  và  $y_A+y_C=y{}_B+y_D$

Lời giải:

Ta có: $\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)$ ,$\overrightarrow{DC}=\left(x_C-x_D;y_C-y_D\right)$

Do ABCD là hình bình hành nên ta có:  $\overrightarrow{AB}=\overrightarrow{DC}$

Hay  $\left\{\begin{array}{l}{x}_B-x_A=x_C-x_D\\ y_B-y_A=y_C-y_D\end{array}\right.\iff \left\{\begin{array}{l}{x}_B+x_D=x_C+x_A\\ y_B+y_D=y_C+y_A\end{array}\right.$

Vậy bài toán được chứng minh.

Bài 11 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng M(1; - 2), N(3; 1), P(- 1; 2). Tìm tọa độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.

Lời giải:

Do tứ giác MNPQ là hình thang có MN // PQ

Nên $\overrightarrow{MN}$  cùng phương với $\overrightarrow{PQ}$ .

Mà PQ = 2MN, $\overrightarrow{MN}$  ngược hướng với $\overrightarrow{PQ}$

Suy ra $\overrightarrow{PQ}=-2.\overrightarrow{MN}$ .

Gọi Q(a; b), ta có: $\overrightarrow{MN}=\left(3-1;1+2\right)=\left(2;3\right)$  và  $\overrightarrow{PQ}=\left(a+1;b-2\right)$

$\overrightarrow{PQ}=-2.\overrightarrow{MN}$ $\iff \left\{\begin{array}{l}a+1=\left(-2\right).2\\ b-2=\left(-2\right).3\end{array}\right.\iff \left\{\begin{array}{l}a=-5\\ b=-4\end{array}\right.$.

Vậy Q(-5; -4).