Giải Toán 7 (Cánh diều) Bài 7: Đại lượng tỉ lệ thuận
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 7 Bài 7: Đại lượng tỉ lệ thuận sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 7. Mời các bạn đón xem:
Mục lục Giải bài tập Toán 7 Bài 7: Đại lượng tỉ lệ thuận
Hoạt động khởi động
Khởi động trang 59 Toán lớp 7 Tập 1: Một chiếc máy bay bay với vận tốc không đổi là 900km/h. 
Lời giải:
Ta sẽ thấy với vận tốc không đổi, nếu máy bay bay quãng đường ngắn thì thời gian sẽ ít còn nếu bay quãng đường dài thì thời gian sẽ nhiều.
Do đó nếu quãng đường bay tăng thì thời gian bay tăng; quãng đường bay giảm thì thời gian bay giảm.
1. Khái niệm
 Lời giải:
Lời giải:
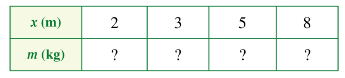
Công thức: m = 2.x.
+) Với x = 2 thì m = 2.2 = 4
+) Với x = 3 thì m = 2.3 = 6
+) Với x = 5 thì m = 2.5 = 10
+) Với x = 8 thì m = 2.8 = 16
Ta có bảng sau:
|
x (m) |
2 |
3 |
5 |
8 |
|
m (kg) |
4 |
6 |
10 |
16 |
Luyện tập 1 trang 60 Toán lớp 7 Tập 1: Một chiếc ô tô chuyển động với vận tốc 65km/h.
a) Viết công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động.
c) Tính giá trị của s khi t = 0,5; t = ; t = 2.
Lời giải:
a) Công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động là:
s = vt = 65t (km)
b) s và t là hai đại lượng tỉ lệ thuận. Hệ số tỉ lệ của s đối với t là 65.
c)
+) Với t = 0,5 thì s = 65.0,5 = 32,5 (km)
+) Với t = thì s = 65. = 97,5 (km)
+ Với t = 2 thì s = 65.2 = 130 (km).
2. Tính chất
Hoạt động 2 trang 60 Toán lớp 7 Tập 1: Cho biết x; y là hai đại lượng tỉ lệ thuận với nhau:
a) Hãy xác định hệ số tỉ lệ của y đối với x.
c) So sánh các tỉ số và ; và .
Lời giải:
a) Vì x và y là hai đại lượng tỉ lệ thuận với nhau nên y = kx (k ≠ 0)
Với x1 = 3, y1 = 9 ta có: 9 = k.3 nên k = 9 : 3 = 3
Vậy hệ số tỉ lệ của y đối với x là 3.
b) Ta có:
nên
c) Ta có: và nên
và nên .
3. Một số bài toán
Lời giải:
Gọi x (phút), y (trang) lần lượt là số phút và số trang in được (x; y > 0).
Khi đó, mối quan hệ giữa số phút và số trang in là hai đại lượng tỉ lệ thuận với nhau.
Áp dụng tính chất tỉ lệ thuận ta có: .
Thay x1 = 5, y1 = 120, x2 = 3 ta có: nên
Vậy trong 3 phút máy in đó in được 72 trang.
Lời giải:
Gọi x, y, z (cây) lần lượt là số cây mỗi lớp 7A; 7B; 7C chăm sóc được (x; y; z ∈ ℕ*)
Vì số cây mỗi lớp chăm sóc tỉ lệ thuận với số học sinh của lớp nên ta có:
x : y : z = 40 : 32 : 36.
Ta có dãy tỉ số bằng nhau: .
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Ta có:
suy ra x = 20 (thoả mãn)
suy ra y = 16 (thoả mãn)
suy ra z = 18 (thoả mãn)
Vậy số cây ba lớp 7A; 7B; 7C chăm sóc lần lượt là 20 cây; 16 cây; 18 cây.
Bài tập
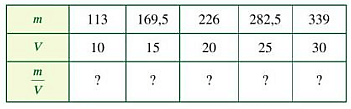
b) Hai đại lượng m và V có tỉ lệ thuận với nhau không? Vì sao?
Lời giải:
a)
+) Với m = 113 và V = 10 nên
+) Với m = 169,5 và V = 15 nên
+) Với m = 226 và V = 20 nên
+) Với m = 282,5 và V = 25 nên
+) Với m = 339 và V = 30 nên
Ta có bảng sau:
|
m |
113 |
169,5 |
226 |
282,5 |
339 |
|
V |
10 |
15 |
20 |
25 |
30 |
|
|
11,3 |
11,3 |
11,3 |
11,3 |
11,3 |
Bài 2 trang 63 Toán lớp 7 Tập 1: Cho biết x,y là hai đại lương tỉ lệ thuận với bảng sau: 
a) Xác định hệ số tỉ lệ của y đối với x. Viết công thức tính y theo x.
b) Xác định hệ số tỉ lệ của x đối với y. Viết công thức tính x theo y.
Lời giải:
a) Vì x, y là hai đại lượng tỉ lệ thuận nên y = kx (k ≠ 0)
Với x = 6; y = 4 nên ta có: 4 = 6.k nên k = 4:6 = .
Hệ số tỉ lệ của y đối với x là .
Công thức tính y theo x là: y = .
b) Theo câu a) y = x
Suy ra x = y
Vậy: Hệ số tỉ lệ của x đối với y là .
Công thức tính x theo y là: x = y.
c) Ta sử dụng y = và x = ta tính được bảng sau:
|
x |
6 |
15 |
21 |
39 |
42 |
|
y |
4 |
10 |
14 |
26 |
28 |
Lời giải:
Gọi x (l), y (g) lần lượt là số lít nước biển và số gam muối có trong số nước biển đó (x; y > 0).
Khi đó, mối quan hệ giữa số lít nước biển và số gam muối có trong số nước biển đó là hai đại lượng tỉ lệ thuận với nhau.
Áp dụng tính chất tỉ lệ thuận ta có: .
Thay ta có:
Do đó
Vậy sẽ có 420 gam muối trong 12 lít nước biển.
Lời giải:
Gọi x (phút), y (sản phầm) lần lượt là số phút và số sản phẩm mà chiếc máy đó làm được (x; y > 0).
Khi đó, mối quan hệ giữa số phút và số sản phẩm mà chiếc máy đó làm được được là hai đại lượng tỉ lệ thuận với nhau.
Áp dụng tính chất tỉ lệ thuận ta có: .
Thay ta có: nên
Vậy để làm được 45 sản phẩm chiếc máy đó cần 20 phút.
 Lời giải:
Lời giải:
Đổi 250 g = 0,25 kg.
Đặt x (kg), y (kg), z (lít) lần lượt là số kg chanh đào, số kg đường phèn và số lít mật ong để làm thuốc ho theo tỉ lệ (x; y; z > 0).
Khi đó mối quan hệ giữa số kg chanh đào, số kg đường phèn và số lít mật ong tỉ lệ thuận với nhau.
Giả sử cần x1 = 0,5 (kg) chanh đào thì cần y1 = 0,25 (kg) đường phèn và và z1 = 0,5 (lít) mật ong.
Cần x2 = 2,5 (kg) chanh đào thì cần y2 (kg) đường phèn và và z2 (lít) mật ong.
• Ta có:
Thay x1 = 0,5; y1 = 0,25; x2 = 2,5 ta có:
Do đó
• Ta có:
Thay ta có:
Do đó
Vậy để ngâm 2,5 kg chanh đào làm thuốc ho theo tỉ lệ thì cần 1,25kg đường phèn và 2,5 lít mật ong.
• 9,9 l/100 km trên đường hỗn hợp;
• 13,9 l/100 km trên đường đô thị;
Lời giải:
a) Với 65 lít xăng, cô Hạnh có thể đi số km đường đô thị là:
65.100:13,9 (km)
Với 65 lít xăng, cô Hạnh có thể đi số km đường hỗn hợp là:
65.100:9,9 (km)
Với 65 lít xăng, cô Hạnh có thể đi số km đường cao tốc là:
65.100:7,5 (km)
b) Để đi quãng đường 400km trên đường đô thị, trong bình xăng của ô tô cô Hạnh phải có tối thiểu số lít xăng là:
400.13,9:100 = 55 (lít)
c) Đi 300km đường hỗn hợp hết số lít xăng là: 300.9,9:100 = 29,7 (lít)
Đi 300km đường cao tốc hết số lít xăng là: 300.7,5:100 = 22,5 (lít)
Để đi quãng đường 300km trên đường hỗn hợp và 300km trên đường cao tốc, trong bình xăng chiếc xe ô tô của cô Hạnh cần tối thiếu số lít xăng là:
29,7 + 22,5 = 52,2 (lít)