Quảng cáo
3 câu trả lời 4863
Phân tích đa thức thành nhân tử
Cho đa thức:
![]()
1. Phân nhóm các hạng tử
Ta nhóm các hạng tử như sau:
![]()
2. Phân tích từng nhóm
- Nhóm thứ nhất:
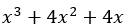 .
.
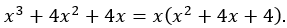
Ta nhận thấy x2 + 4x + 4 là một hàng đẳng thức đáng nhớ:
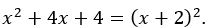
Vậy:
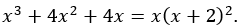
- Nhóm thứ hai: -xy2 không cần phân tích thêm.
3. Kết hợp kết quả
Thay vào biểu thức ban đầu, ta có:
![]()
4. Đưa x ra làm nhân tử chung
Ta nhận thấy cả hai hạng tử đều chứa , do đó, đặt ra ngoài:
![]()
5. Sử dụng hàng đẳng thức hiệu hai bình phương
Biểu thức trong ngoặc vuông là hiệu của hai bình phương:
![]()
6. Kết quả cuối cùng
Thay vào, ta được:
![]()
Kết luận
Biểu thức đã phân tích thành nhân tử là:
![]()
\[\begin{array}{l}
{x^3} + 4{x^2} + 4x - x{y^2}\\
= x\left( {{x^2} + 4{\rm{x}} + 4 - {y^2}} \right)\\
= x\left[ {{{\left( {x + 2} \right)}^2} - {y^2}} \right]\\
= x\left( {x + 2 - y} \right)\left( {x + 2 + y} \right)
\end{array}\]
phân tích đa thức thành nhân tử:
a,x^3-4x^2+4x-xy^2
b,x^3 -4x^2 +121x-27
c,3x^2 -7x -10
d,5x^3 -5x^2y -10x^2 +10xy
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


