Cho ABC vuôn tại A , đường cao AH. Biết AB = 15cm , BC = 25cm.
a) Tính độ dài cạnh AC , tính số đó góc B ( góc làm tròn đến độ )
b) Gọi M,N lần lượt là hình chiếu của H trên AB,AC . Chứng minh MA.AB = AN.AC
Quảng cáo
1 câu trả lời 1786
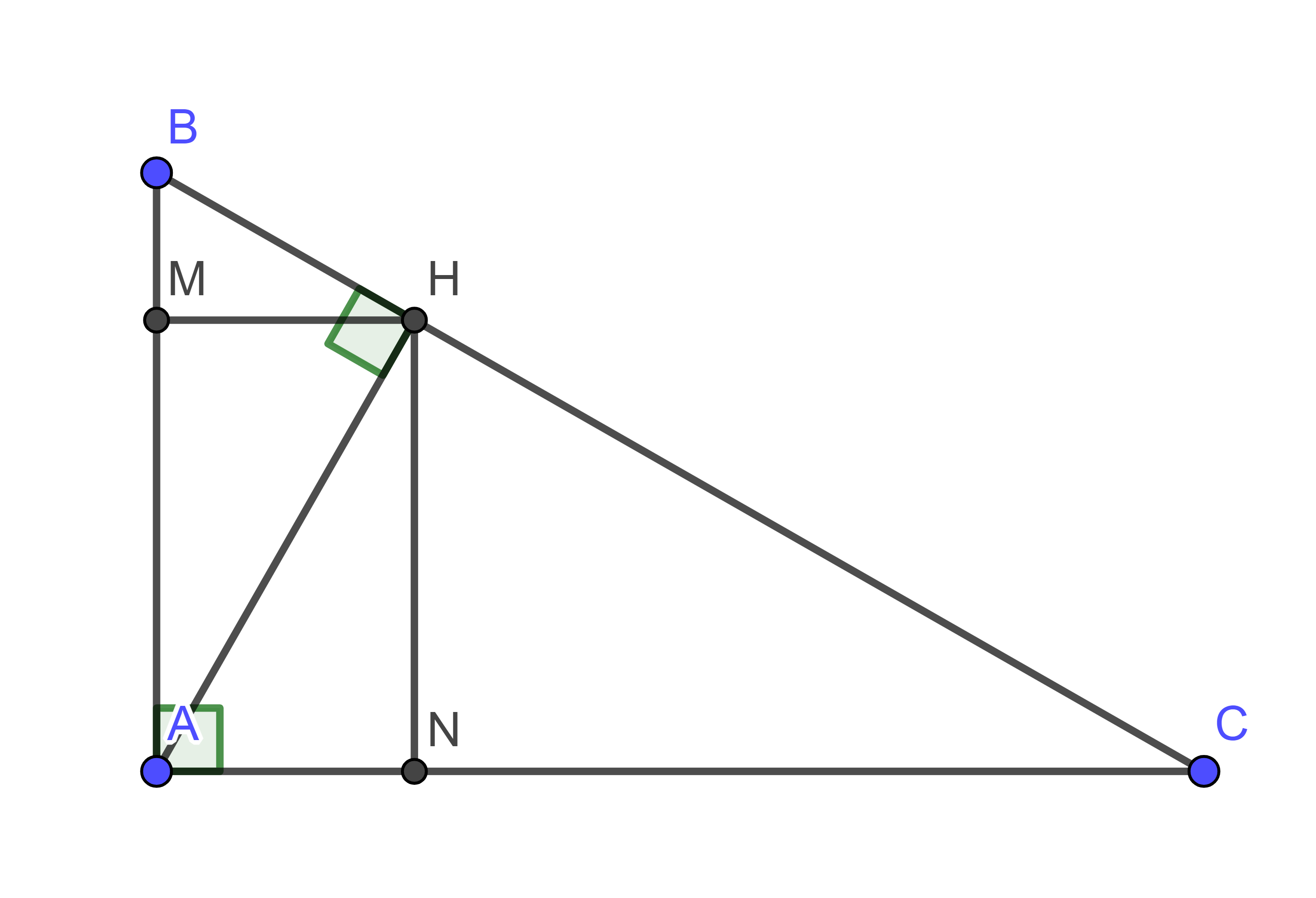
a) Xét tam giác ABC vuông tại A đường cao AH
Theo Pyta go:
\[\begin{array}{l}
A{B^2} + A{C^2} = B{C^2}\\
= > AC = \sqrt {{{25}^2} - {{15}^2}} = 20\left( {cm} \right)\\
\cos B = \frac{{AB}}{{BC}} = \frac{{15}}{{25}} = \frac{3}{5}\\
= > \widehat B \approx {53^o}\\
vay:AC = 20\left( {cm} \right);\widehat B \approx {53^o}
\end{array}\]
b) Xét tam giác BAH vuông tại H đường cao HM
Theo hệ thức lượng tam giác vuông:
\[MA.AB = A{H^2}\]
Xét tam giác \CAH vuông tại H đường cao HN
Theo hệ thức lượng tam giác vuông:
\[NA.AC = A{H^2}\]
vậy MA.AB=NA.AC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


