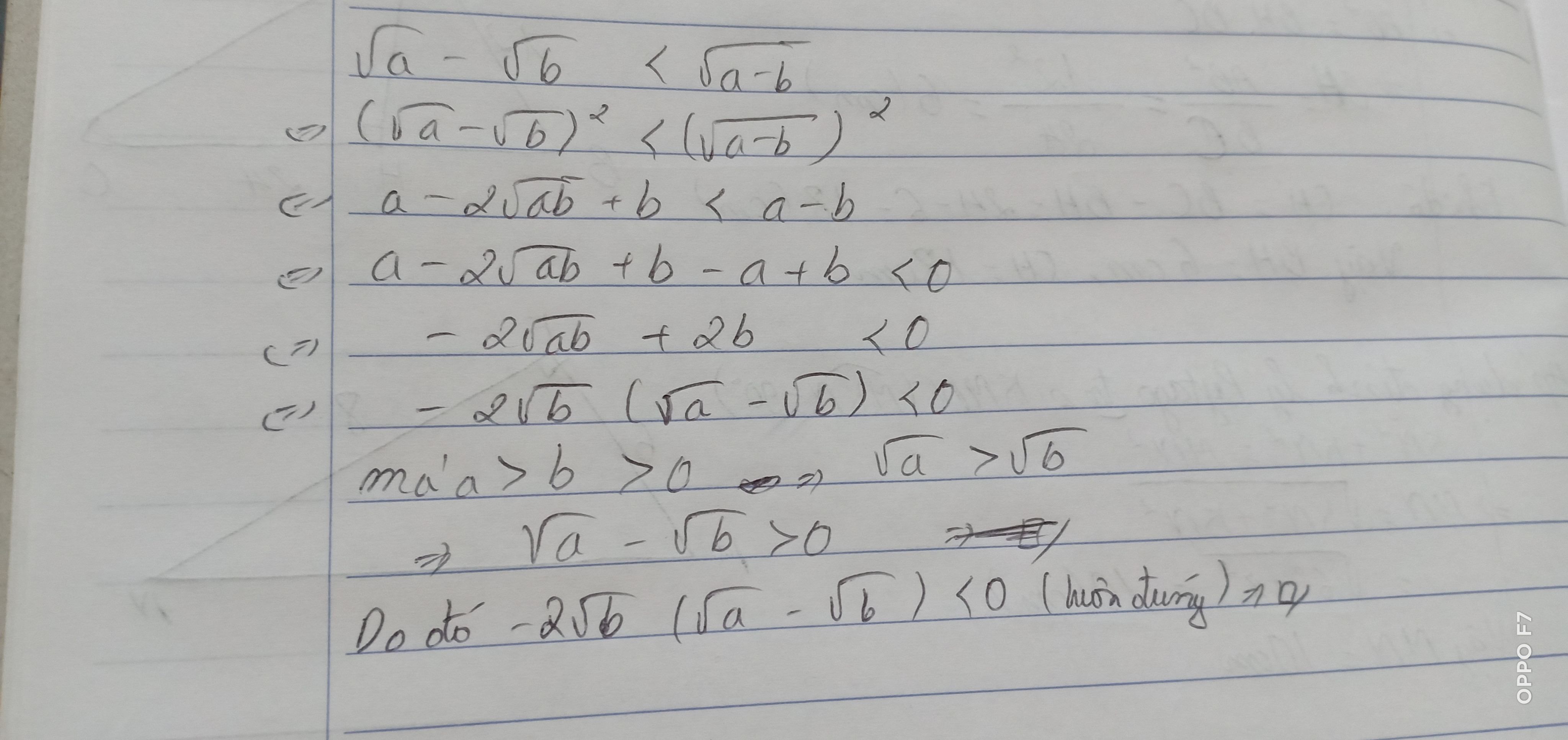Khánh Linh
Hỏi từ APP VIETJACK
Chứng minh rằng , với a>b>0 thì căn a - căn b< căn a-b
Quảng cáo
2 câu trả lời 2224
\[\begin{array}{l}
Voi:\\
a > b > 0\\
= > \sqrt a > \sqrt b \\
= > \sqrt b - \sqrt a < 0\\
\sqrt a - \sqrt b < \sqrt {a - b} \\
\Leftrightarrow {\left( {\sqrt a - \sqrt b } \right)^2} < {\left( {\sqrt {a - b} } \right)^2}\\
\Leftrightarrow a - 2\sqrt {ab} + b < a - b\\
\Leftrightarrow a - 2\sqrt {ab} + b - a + b < 0\\
\Leftrightarrow 2b - 2\sqrt {ab} < 0\\
\Leftrightarrow 2\sqrt b \left( {\sqrt b - \sqrt a } \right) < 0\left( 1 \right)\\
do:\sqrt b > 0\\
\sqrt b - \sqrt a < 0
\end{array}\]
=> 1 luôn đúng
Vậy Với a>b>0 thì \[\sqrt a - \sqrt b < \sqrt {a - b} \]
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211
Gửi báo cáo thành công!