Quảng cáo
1 câu trả lời 11263
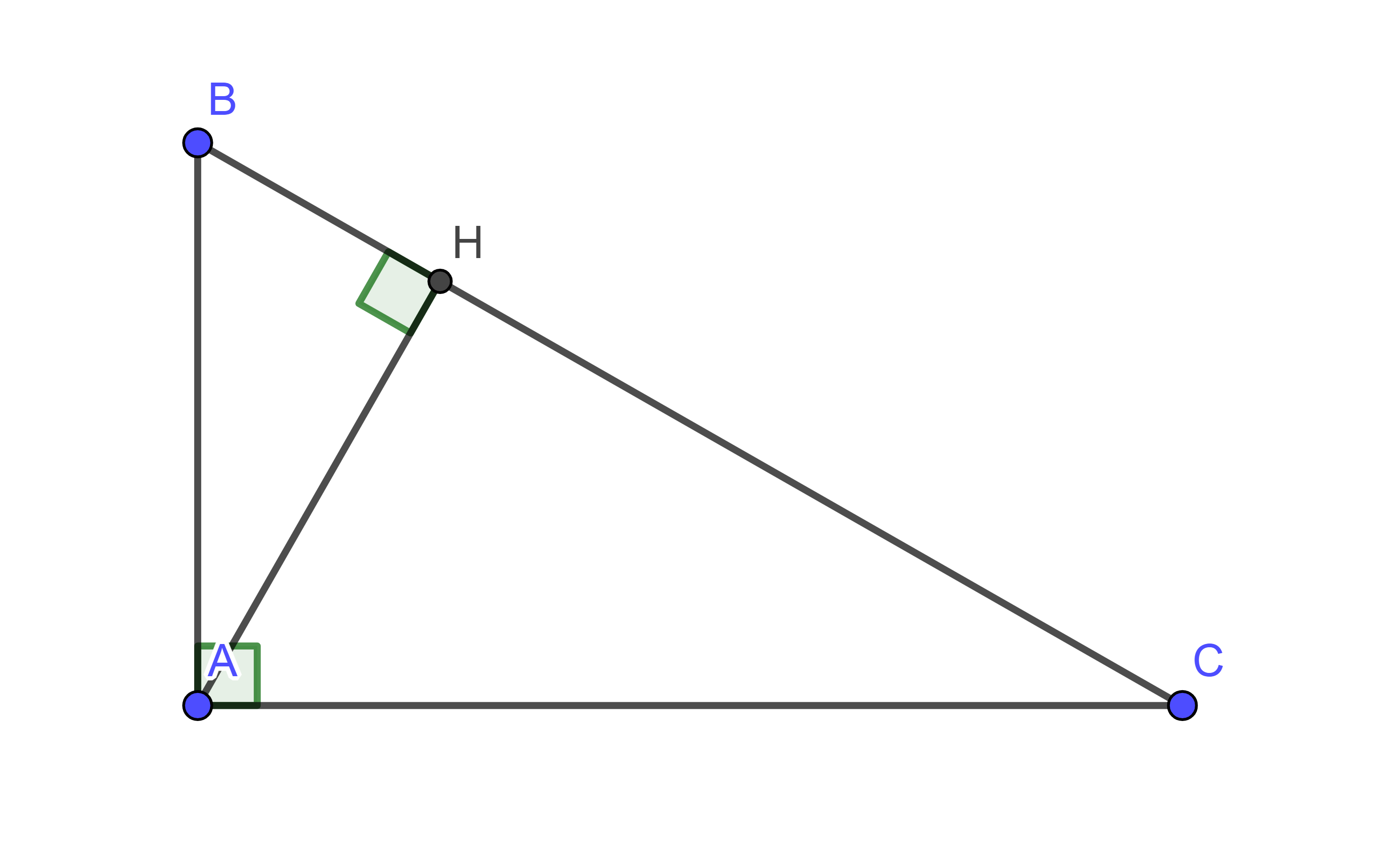
xét tam giác BAC vuông tại A đường cao AH
Theo pytago:
\[\begin{array}{l}
B{C^2} = A{B^2} + A{C^2}\\
= > AC = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)
\end{array}\]
Áp dụng hệ thức lượng tam giác vuông:
\[\begin{array}{l}
+ )A{B^2} = BH.BC\\
= > BH = \frac{{{3^2}}}{5} = 1,8\left( {cm} \right)\\
+ )A{C^2} = CH.BC\\
= > CH = \frac{{{4^2}}}{5} = 3,2\left( {cm} \right)\\
+ )AB.AC = AH.BC\\
= > AH = \frac{{3.4}}{5} = 2,4\left( {cm} \right)
\end{array}\]
Vậy BH= 1,8cm; CH =3,2cm, AC=4cm và AH=2,4cm
tuan khanh
· 3 năm trước
Cho tam giác ABC vuông tại A có AB= 3cm;BC 5cm a.Tính độ dài đoạn AC b.Trên tia đối của tia AB lấy D sao cho AD = AB Chứng minh rằng :tam giácACD=tam giácACB và từ đó suy ra tam giácCBD c.Từ A kẻ vuông góc xuống CB tại E, kẻ vuông góc xuống CD tại F Chứng Minh rằng:EF//BD
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490
Gửi báo cáo thành công!


