Cho tam giác ABC vuông tại A,có AC > AB và đường cao AH. Gọi D,E lần lượt là hình chiếu của H trên AB,AC
1,Cm AD.AB = AE.AC và tam giác ABC đồng dạng với AED.
2,Cho biết BH=2cm;HC=4.5 cm
3,tính độ dài đoạn thẳng DE
4,tính số đo góc ABC (làm tròn đến độ)
5,tính diện tích tam giác ADE
Quảng cáo
1 câu trả lời 2020
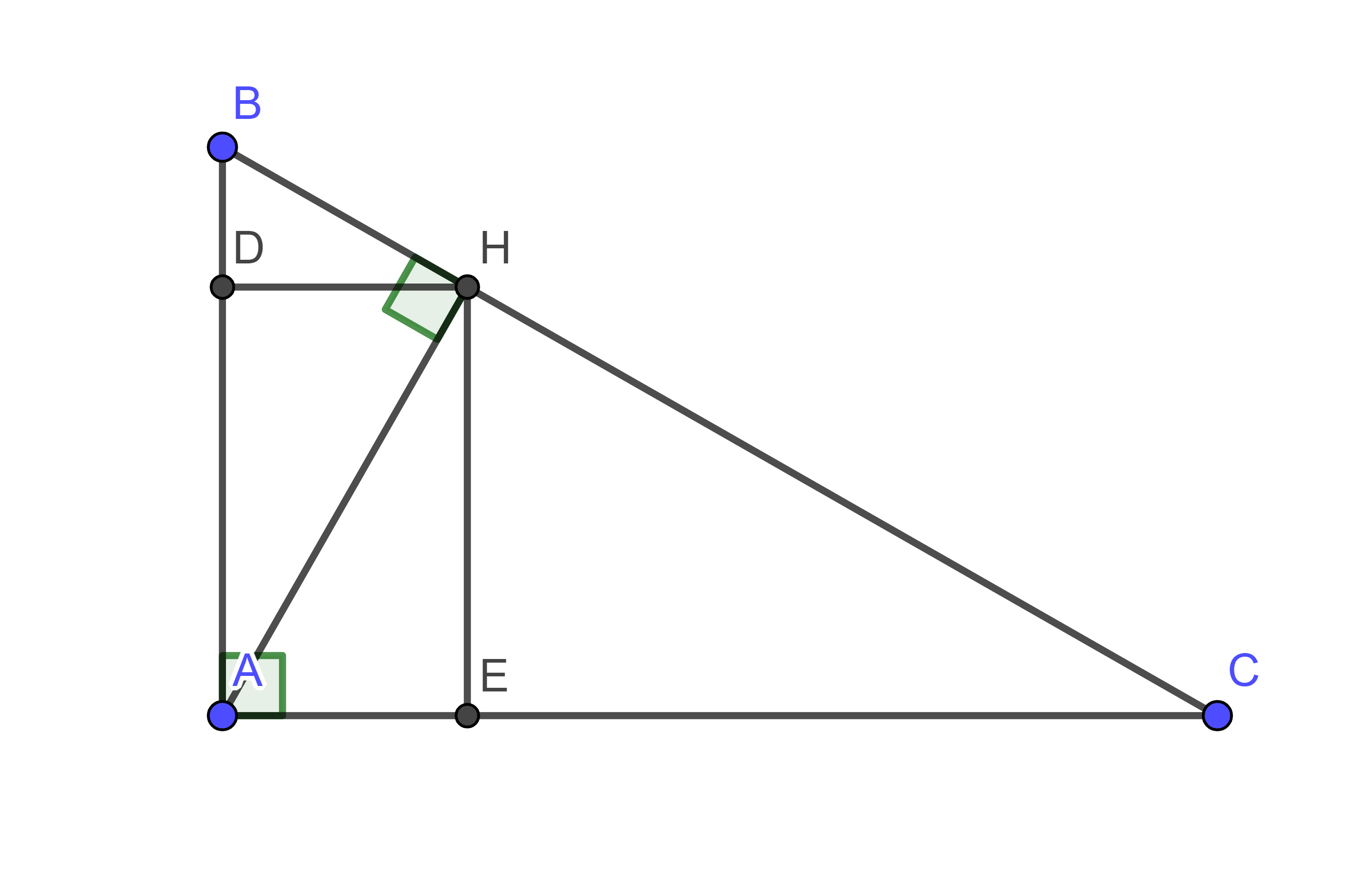
1) Xét tam giác ABH vuông tại H có đường cao HD
Áp dụng hệ thức lượng tam giác vuông:
\[AB.AD = A{H^2}\]
xét tam giác AHCvuông tại H có đường cao HE
Áp dụng hệ thức lượng tam giác vuông:
\[AC.AE = A{H^2}\]
=> AB.AD=AC.AE
=> \[\frac{{AB}}{{AE}} = \frac{{AC}}{{AD}}\]
xét tam giác ADE và tam giác ACB có:
\[\frac{{AB}}{{AE}} = \frac{{AC}}{{AD}}\]
Góc A chung
=> Tam giác ADE đồng dạng tam giác ACB (c-g-c)
3) xét tứ giác ADHE có góc ADH=góc AEH=góc DAE=90 dộ
=>Tứ giác ADHE là hcn
=> AH =DE (tính chất hcn)
Xét tam giác ABc vuông tại A có đường cao AH
Áp dụng hệ thức lượng tam giác vuông:
\[\begin{array}{l}
A{H^2} = BH.HC = 2.4,5 = 9\\
= > AH = 3\left( {cm} \right)
\end{array}\]
=> DE=3 cm
4) xét tam giác BAH vuông tại H có:
\[\begin{array}{l}
\tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{3}{2}\\
= > \widehat {ABH} \approx {56^o}
\end{array}\]
Vậy \[\widehat {ABC} = {56^o}\]
5) ta có: BC=BH+HC=2+4,5=6,5 cm
\[{S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.3.6,5 = 9,75\left( {c{m^2}} \right)\]
ta có: Tam giác ADE đồng dạng tam giác ACB
\[\begin{array}{l}
= > \frac{{{S_{ADE}}}}{{{S_{ABC}}}} = {\left( {\frac{{DE}}{{BC}}} \right)^2} = {\left( {\frac{3}{{6,5}}} \right)^2} = \frac{{36}}{{169}}\\
= > {S_{ADE}} = \frac{{36}}{{169}}.9,75 = \frac{{27}}{{13}}\left( {c{m^2}} \right)\\
vay:{S_{ADE}} = \frac{{27}}{{13}}\left( {c{m^2}} \right)
\end{array}\]
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


