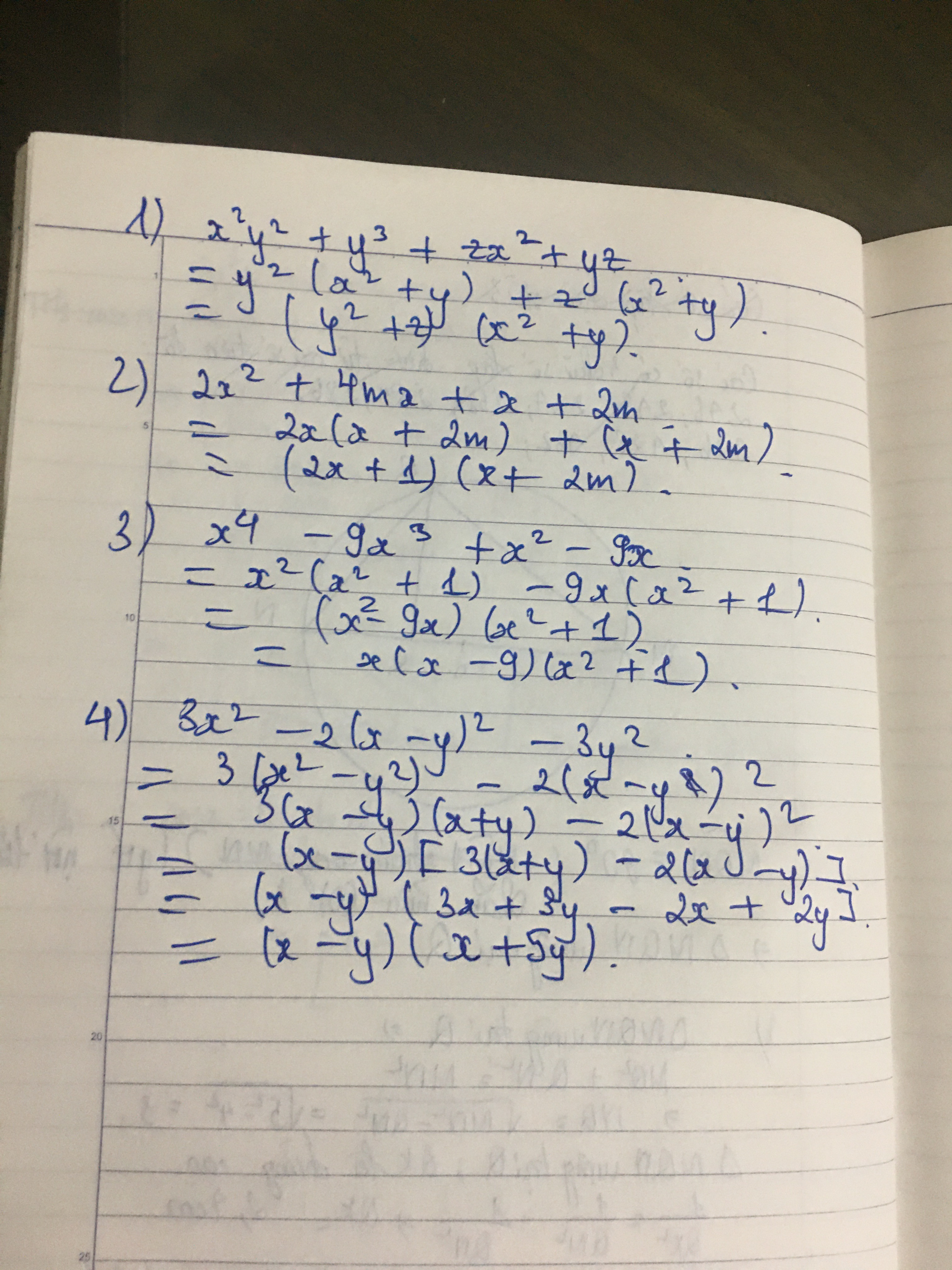Quảng cáo
2 câu trả lời 394
1)x2y2+y3+zx2+yz=(x2y2+y3)+(zx2+yz)=y2(x2+y)+z(x2+y)=(x2+y)(y2+z)2)2x2+4mx+x+2m=2x(x+2m)+(x+2m)=(x+2m)(2x+1)3)x4−9x3+x2−9x=x(x3−9x2+x−9)=x[x2(x−9)+(x−9)]=x(x−9)(x2+1)4)3x2−2(x−y)2−3y2=(3x2−3y2)−2(x−y)2=3(x−y)(x+y)−2(x−y)2=(x−y)(3x+3y−2x+2y)=(x−y)(x+5y)
Quảng cáo
Câu hỏi hot cùng chủ đề
-
101711
-
Hỏi từ APP VIETJACK53271
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức
=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
43308