cho tam giác abc và đường trung tuyến bd , ce cắt nhau tại G . gọi m, n lần lượt là trung điểm của bg , cg . cm tg mnde là hbh
Quảng cáo
5 câu trả lời 1367
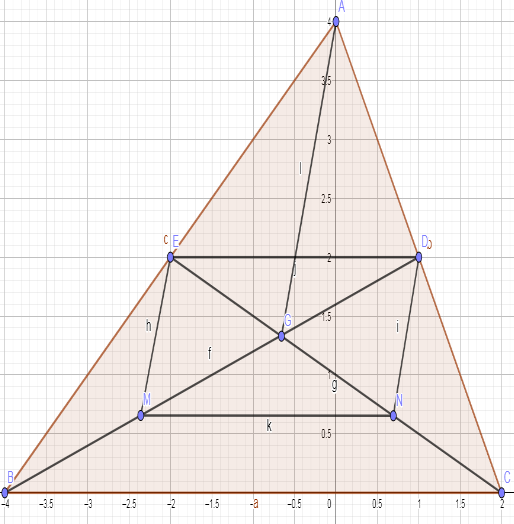
Trong tam giác ABC , có :
EA = EB ( CE là trung tuyến )
DA = DC ( DB là trung tuyến )
=> ED là đường trung bình của tam giác ABC
=> ED // BC (1) , DE = 1/2 BC (2)
Trong tam giác GBC , có :
MG = MB ( gt)
NG = NC ( gt)
=> MN là đương trung bình của tam giác GBC
=> MN // BC (3) , MN = 1/2 BC (4)
Từ 1 và 2 => ED // MN ( * )
Từ 3 và 4 => ED = MN ( **)
Từ * và ** => EDMN là hbh
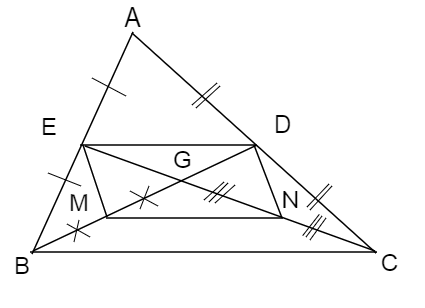
Trong tam giác ABC , có :
EA = EB ( CE là trung tuyến )
DA = DC ( DB là trung tuyến )
=> ED là đường trung bình của tam giác ABC
=> ED // BC (1) , DE = 1/2 BC (2)
Trong tam giác GBC , có :
MG = MB ( gt)
NG = NC ( gt)
=> MN là đương trung bình của tam giác GBC
=> MN // BC (3) , MN = 1/2 BC (4)
Từ 1 và 2 => ED // MN ( * )
Từ 3 và 4 => ED = MN ( **)
Từ * và ** => EDMN là hbh ( DHNB )
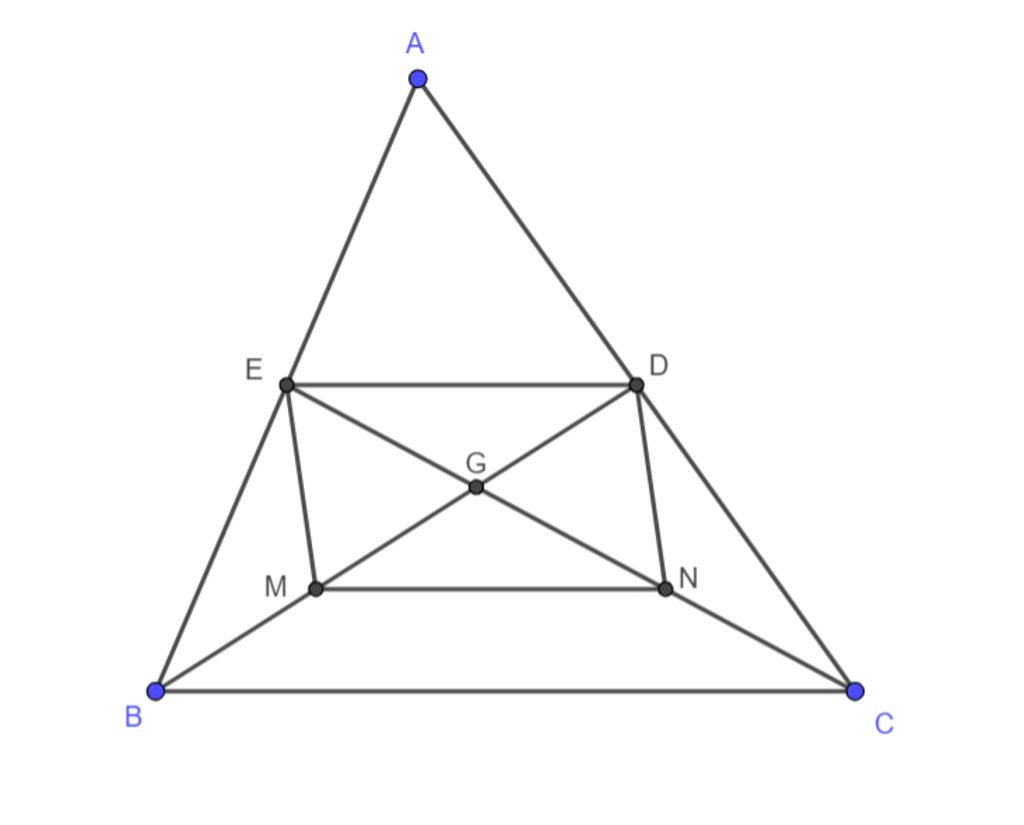
a, Xét tam giác ABC có AE=EB (gt), AD=DC (gt)
⇒ED là đường trung bình của tam giác ABCABC
⇒ ED//BC và ED=1/2BC
Xét tam giác BGC có BM=MG (gt), CN=NG (gt)
⇒MN là đường trung bình của tam giác BGC
⇒MN // BC và MN=1/2BC
Có MN//BC mà ED//BC ⇒ MN//ED
MN=1/2BC,ED=1/2BC⇒MN=ED
Tứ giác MNDE có: MN//ED, MN=ED
⇒ MNDE là hình bình hành
Trong tam giác ABC , có :
EA = EB ( CE là trung tuyến )
DA = DC ( DB là trung tuyến )
=> ED là đường trung bình của tam giác ABC
=> ED // BC (1) , DE = 1/2 BC (2)
Trong tam giác GBC , có :
MG = MB ( gt)
NG = NC ( gt)
=> MN là đương trung bình của tam giác GBC
=> MN // BC (3) , MN = 1/2 BC (4)
Từ 1 và 2 => ED // MN ( * )
Từ 3 và 4 => ED = MN ( **)
Từ * và ** => EDMN là hbh
Quảng cáo













