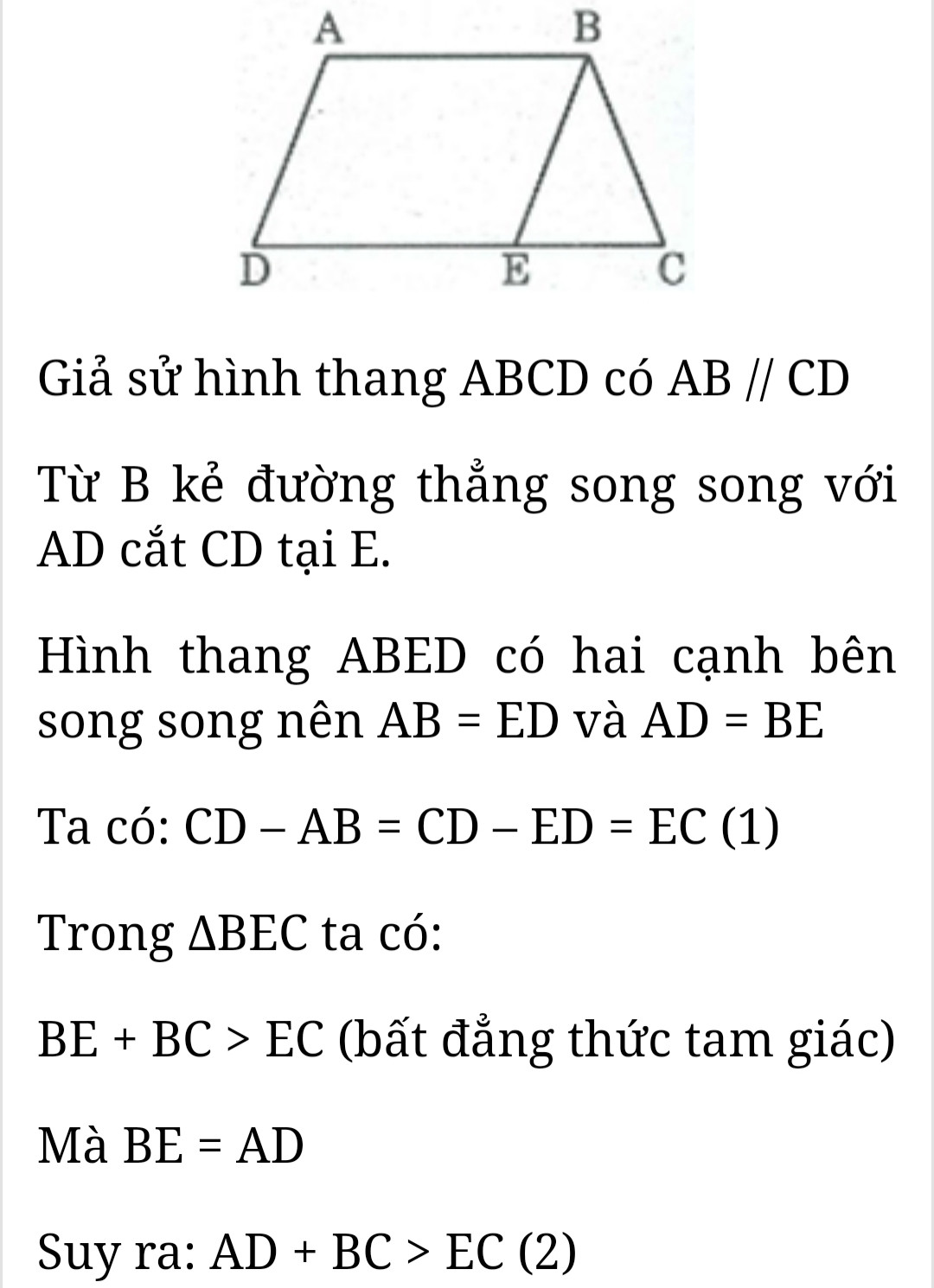
Cho một hình thang có 2 đáy không bằng nhau. Chứng minh rằng: a, Tổng 2 góc kề đáy nhỏ lớn hơn tổng hai góc kề đáy lớn b, Tổng hai cạnh bên lớn hơn hiệu hai đáy
Quảng cáo
2 câu trả lời 5963
Cho hình thang ABCDABCDABCD (với AB∥CDAB \parallel CDAB∥CD) có hai đáy không bằng nhau, giả sử AB<CDAB < CDAB<CD.
Chứng minh rằng:
a) Tổng hai góc kề đáy nhỏ lớn hơn tổng hai góc kề đáy lớn.
b) Tổng hai cạnh bên lớn hơn hiệu hai đáy.
Bài làm
1. Phân tích hình vẽ và giả thiết
Giả sử hình thang ABCDABCDABCD có:
AB∥CDAB \parallel CDAB∥CD
AB<CDAB < CDAB<CD (⇒ ABABAB là đáy nhỏ, CDCDCD là đáy lớn)
Khi đó:
Hai góc kề đáy nhỏ: ∠A\angle A∠A và ∠B\angle B∠B
Hai góc kề đáy lớn: ∠C\angle C∠C và ∠D\angle D∠D
a) Chứng minh: ∠A+∠B>∠C+∠D\angle A + \angle B > \angle C + \angle D∠A+∠B>∠C+∠D
Chứng minh:
Vì AB∥CDAB \parallel CDAB∥CD, ta có:
∠A+∠D=180∘(hai goˊc trong cuˋng phıˊa)\angle A + \angle D = 180^\circ \quad \text{(hai góc trong cùng phía)}∠A+∠D=180∘(hai goˊc trong cuˋng phıˊa)và
∠B+∠C=180∘\angle B + \angle C = 180^\circ∠B+∠C=180∘Cộng hai đẳng thức:
(∠A+∠B)+(∠C+∠D)=360∘(\angle A + \angle B) + (\angle C + \angle D) = 360^\circ(∠A+∠B)+(∠C+∠D)=360∘Suy ra:
∠A+∠B=360∘−(∠C+∠D)\angle A + \angle B = 360^\circ - (\angle C + \angle D)∠A+∠B=360∘−(∠C+∠D)Nếu đáy nhỏ ABABAB ngắn hơn đáy lớn CDCDCD, thì cạnh bên của hình thang nghiêng hơn (hình thang “dốc hơn”), do đó hai góc ở đáy nhỏ lớn hơn hai góc ở đáy lớn.
Nói cách khác, ∠A+∠B>∠C+∠D\angle A + \angle B > \angle C + \angle D∠A+∠B>∠C+∠D.
👉 Kết luận:
∠A+∠B>∠C+∠D\boxed{\angle A + \angle B > \angle C + \angle D}∠A+∠B>∠C+∠D
b) Chứng minh: AD+BC>CD−ABAD + BC > CD - ABAD+BC>CD−AB
Cách chứng minh hình học
Dựng hai đường cao từ AAA và BBB xuống đáy lớn CDCDCD, lần lượt tại HHH và KKK.
Gọi hhh là chiều cao của hình thang. Khi đó:
HK=CD−ABHK = CD - ABHK=CD−ABXét hai tam giác vuông ADHADHADH và BCKBCKBCK:
AD=h2+DH2AD = \sqrt{h^2 + DH^2}AD=h2+DH2
BC=h2+CK2BC = \sqrt{h^2 + CK^2}BC=h2+CK2
Mà DH+CK=CD−AB=HKDH + CK = CD - AB = HKDH+CK=CD−AB=HK.
Theo bất đẳng thức tam giác trong mỗi tam giác vuông và tính chất của căn bậc hai, ta có:
AD+BC>DH+CK=CD−ABAD + BC > DH + CK = CD - ABAD+BC>DH+CK=CD−AB👉 Kết luận:
AD+BC>CD−AB\boxed{AD + BC > CD - AB}AD+BC>CD−AB
✅ Kết luận chung
Với hình thang ABCDABCDABCD có hai đáy không bằng nhau (AB<CDAB < CDAB<CD):
{∠A+∠B>∠C+∠DAD+BC>CD−AB\begin{cases} \angle A + \angle B > \angle C + \angle D \\ AD + BC > CD - AB \end{cases}{∠A+∠B>∠C+∠DAD+BC>CD−AB
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
9952
Đã trả lời bởi chuyên gia
9952 -
 Đã trả lời bởi chuyên gia
7791
Đã trả lời bởi chuyên gia
7791