Cho tam giác ABC, các đường cao BH và CE cắt nhau tại H. Chứng minh rằng
a) AE.AB=AD.AC. b)AED=ACD
c)Tính diện tích tgiác ABC biết AC=6cm, BC=5cm, CD=3cm
d) BE.BA+CD.CA=BC^2
Quảng cáo
1 câu trả lời 10277
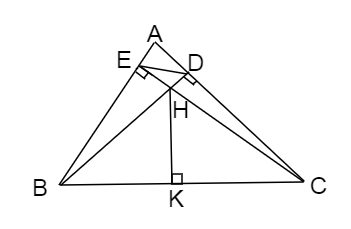
a) Xét △ AEC vuông tại E và △ ADB vuông tại D có:
EAD^ chung
⇒△ AEC đồng dạng với △ ADB(g-g)
⇒⇒ AE/AD=AC/AB
⇒ AE.AB=AC.AD
b) Xét △ AED và △ ACB có:
EAD^ chung
AE/AD=AC/AB
⇒△ AED đồng dạng với △ ACB(c-g-c)
⇒ AED^=ACB^
c)Xét tam giác vuông BCD có:
BC2=BD2+DC2=>BD=√BC2−DC2=√52−32=4(cm)=>SABC=12.BD.AC=12.4.6=12(cm2)
d) Từ H kẻ đưởng vuông góc với BC cắt BC tại K
Xét △ BKH vuông tại K và △ BDC vuông tại D có:
HBK^ chung
⇒△ BKH đồng dạng với △ BDC (g-g)
⇒⇒ BK/BD=BH/BCB
⇒ BK.BC=BH.BD(1)
Xét △ CKH vuông tại K và △ CEB vuông tại D có:
HCK^ chung
⇒△ CKH đồng dạng với △ CEB (g-g)
⇒ CK/CE=CH/BC
⇒ CK.BC=CE.CH(2)
Lấy (1)+(2),ta được:
BH.BD+CH.CE=BK.BC+CK.BC=BC.(CK+BK)=BC.BC=BC^2
Quảng cáo
Câu hỏi hot cùng chủ đề
-
100810
-
Hỏi từ APP VIETJACK51078
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức
=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
42974









