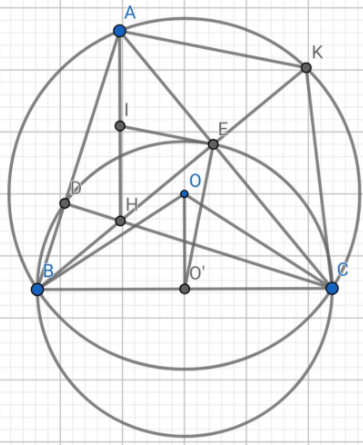
Cho ΔABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Đường tròn đường kính BC tâm O' cắt AB, AC tại D và E, nối BE cắt CD tại H.
a) Chứng minh: AD. AB = AE. AC.
b) Chứng minh: Tứ giác ADHE nội tiếp. Gọi I là tâm đường tròn ngoại tiếp tứ giác này. Chứng minh: IE là tiếp tuyến của (O').
c) Gọi K là điểm đối xứng của H qua AC. Chứng minh: K ∈ (O). d) Cho BC = R √3 . Tính theo R diện tích phần hình tròn (O') nằm ngoài (O).
Quảng cáo
1 câu trả lời 725
a) Ta có:

⇒AD.AB=AE.AC
b) Xét tứ giác ADHE có:
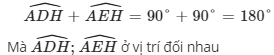
⇒ADHE nội tiếp đường tròn tâm I với I là trung điểm AH
⇒EI là trung tuyến ΔAEH vuông tại E
⇒EI=AI=HI=1/2AH
⇒ΔAEI cân tại I
![]()
Gọi F là giao điểm của AH và BC
ΔABC có H là giao điểm hai đường cao BE; CD
⇒H là trực tâm ΔABC
⇒AH⊥BC tại F
⇒ΔAFC vuông tại F
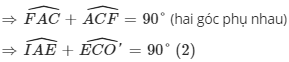
Vì O′ là trung điểm BC (do BC là đường kính của (O′))
⇒EO' là trung tuyến ΔBCE vuông tại E
⇒EO'=CO'=1/2BC
⇒ΔO'CE cân tại O′
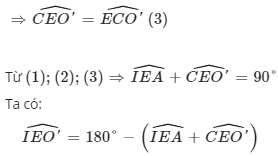
=180°−90°=90°
⇒IE⊥O′E
Mà O′E là bán kính của (O′)
⇒IE là tiếp tuyến tại E của (O′)
c) Xét ΔCHK có:
CE⊥HK tại E
EH=EK (do H và K đối xứng qua AC)
⇒CE vừa là đường cao và trung tuyến ΔCHK
⇒ΔCHK cân tại C
![]()
Vì ADHE nội tiếp (câu b)

⇒BAKC nội tiếp (vì có 2 đỉnh kề nhau A; K cùng nhìn cạnh BC dưới góc vuông)
Mà ΔABCnội tiếp (O)
⇒K∈(O)
d) Vì BC là đường kính của (O′)
⇒O′ là trung điểm BC
![]()
Ta có: OO′⊥BC tại O′ (đường nối tâm vuông góc tại trung điểm dây cung)
⇒ ΔOO′B vuông tại O′
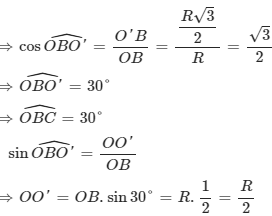
Xét ΔOBC có:
OB=OC=R
⇒ΔOBC cân tại O
![]()
Diện tích hình quạt tròn tạo bởi hai bán kính OB; OC và cung nhỏ BC là:
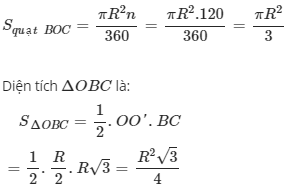
Diện tích hình viên phân tạo bởi cung BC và dây BC là:

Diện tích phần hình tròn (O′) nằm ngoài (O) là:
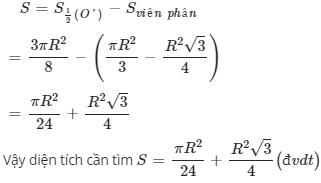
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


