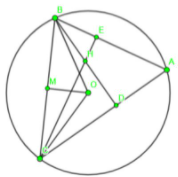
Cho đường tròn (O; R) dây cung BC cố định (BC < 2R) và điểm A di động trên cung lớn BC sao cho tam giác ABC có ba góc nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại H.
a. Chứng minh tứ giác ADHE nội tiếp.
b. Giả sử góc BAC = 60°, hãy tính khoảng cách từ tâm O đến cạnh BC theo R?
Quảng cáo
1 câu trả lời 11687
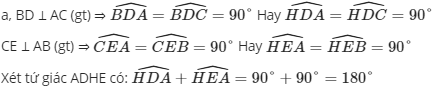
Mà hai góc này ở vị trí đối nhau
⇒ Tứ giác ADHE nội tiếp đường tròn đường kính AH
b, Kẻ OM ⊥ BC
Xét (O) có:

Xét (O) có: OB = OC = R
Xét ΔOBC có: OB = OC (cmt)
⇒ ΔOBC cân tại O
Mà OM ⊥ BC (cmt)
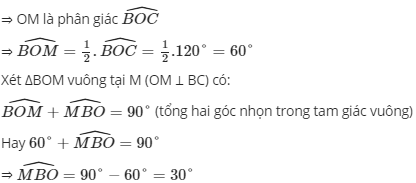
Áp dụng tỉ số lượng giác trong ΔOBM vuông tại M (OM ⊥ BC) có:
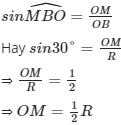
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274
Gửi báo cáo thành công!


