Quảng cáo
1 câu trả lời 6940
Ta có:
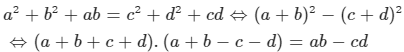
Giả sử ngược lại, p=a+b+c+d là số nguyên tố
Từ ab−cd=p.(a+b−c−d) ta có :
(ab-cd) chia hết p ⇒ab+c.(a+b+c)p đồng dư 0 (mod p)
⇒(a+c).(c+b) đồng dư 0 (mod p)
Nhưng điều này vô lí vì p là số nguyên tố và a, b, c, d>0 nên 0<c+a, c+b< p
⇒(c+a,p) =1⇒ không thể đồng dư 0 (mod p)
Vậy a+b+c+da+b+c+d là hợp số
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211
Gửi báo cáo thành công!


