Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Chứng minh : tứ giác AOHC nội tiếp.
b) Chứng minh : AC.AE= AD.CE
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM//BN
Quảng cáo
1 câu trả lời 34
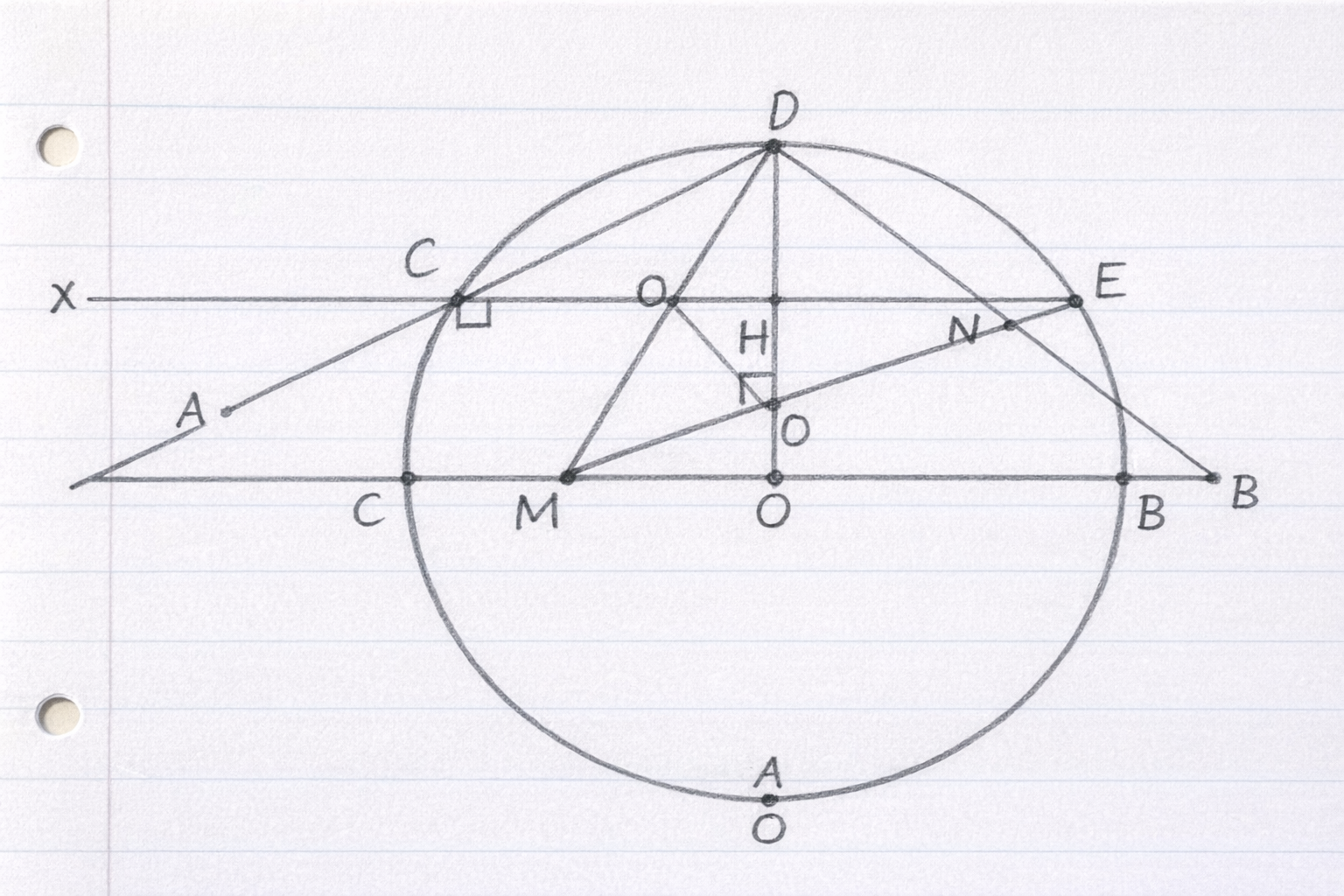
Ta có:
- Ax là tiếp tuyến tại A
- CDE là cát tuyến
Theo định lý tiếp tuyến – cát tuyến:
Mặt khác do C,D,E thẳng hàng: CE=CD+DE
Ta xét hai tam giác:
Ta có:
Suy ra:
c) Chứng minh
Ta có: AB là đường kính
Vì D,E đối xứng qua CO nên:
Mà:
Suy ra: ∠MBA=∠ABN
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104666
Đã trả lời bởi chuyên gia
104666 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69578
Đã trả lời bởi chuyên gia
69578 -
 Đã trả lời bởi chuyên gia
57547
Đã trả lời bởi chuyên gia
57547 -
 Đã trả lời bởi chuyên gia
48088
Đã trả lời bởi chuyên gia
48088 -
 Đã trả lời bởi chuyên gia
47019
Đã trả lời bởi chuyên gia
47019 -
 Đã trả lời bởi chuyên gia
37490
Đã trả lời bởi chuyên gia
37490 -
 Đã trả lời bởi chuyên gia
36573
Đã trả lời bởi chuyên gia
36573


