Cho tam giác ABC ( AB < AC ) có ba góc nhọn ; các đường cao AD ; BK ; CE. Hai đường thẳng EK và BC cắt nhau tại điểm M. CMR BM.ED = BD.EM
Quảng cáo
1 câu trả lời 45
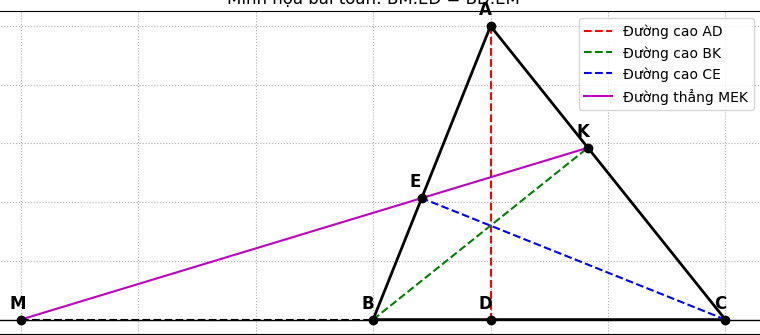
- Xét tứ giác BEDC có (do CE, AD là các đường cao).
- Hai đỉnh E, D cùng nhìn cạnh BC dưới một góc 90 nên BEDC là tứ giác nội tiếp.
- Tương tự, xét tứ giác CKDA có
=> Tứ giác CKDA nội tiếp.
- Xét tứ giác AKEB có
=> Tứ giác AKEB nội tiếp.
- Từ tứ giác nội tiếp BEDC, ta có: = (cùng chắn cung EB).
- Từ tứ giác nội tiếp CKDA, ta có: = (cùng chắn cung KC).
Mà (vì cùng phụ với trong các tam giác vuông CEB và KAB).
=> .
- Ta có AD BC tại D. Gọi tia Dx là tia đối của tia DB.
- Vì .
=> DA là tia phân giác của .
- Vì DA là phân giác trong của tại đỉnh D và DB DA (do AD BC).
=> DB là tia phân giác ngoài của DEK tại đỉnh D.
=> Áp dụng tính chất đường phân giác ngoài cho tam giác DEK với điểm M nằm trên đường thẳng chứa cạnh đối diện:
- Theo tính chất tam giác đồng dạng từ các tứ giác nội tiếp: BDE KDC (g.g)
=> .
- Từ các tỉ số đồng dạng và tính chất phân giác, ta có:
=> BM.ED = BD.EM (Điều phải chứng minh).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104515
Đã trả lời bởi chuyên gia
104515 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69452
Đã trả lời bởi chuyên gia
69452 -
 Đã trả lời bởi chuyên gia
57398
Đã trả lời bởi chuyên gia
57398 -
 Đã trả lời bởi chuyên gia
47987
Đã trả lời bởi chuyên gia
47987 -
 Đã trả lời bởi chuyên gia
46330
Đã trả lời bởi chuyên gia
46330 -
 Đã trả lời bởi chuyên gia
37376
Đã trả lời bởi chuyên gia
37376 -
 Đã trả lời bởi chuyên gia
36313
Đã trả lời bởi chuyên gia
36313


