Quảng cáo
1 câu trả lời 647
Gọi $O$ là trung điểm của $AB$, $I$ là trung điểm của $OA$ ⇒ $IA =
Do $CD \perp OA$ tại $I$, nên $CD$ là dây vuông góc với bán kính tại trung điểm ⇒ $CD$ nằm trong đường tròn, và D, C đối xứng nhau qua OA.
Lấy $E$ trên đoạn $IC$, kẻ tia $AE$ cắt đường tròn tại $F$.
Ta cần tối đa hóa độ dài $DF$.
Xét tam giác $DAE$, điểm $F$ nằm trên đường tròn, là giao điểm thứ hai của tia $AE$ với đường tròn.
Để $DF$ lớn nhất, thì khoảng cách từ D đến điểm F trên tia $AE$ là lớn nhất
⇔ $DF$ vuông góc với $AE$
⇔ Tam giác $DFE$ vuông tại D
Mà D cố định, F thay đổi theo AE ⇒ góc $DFE$ = 90° ⇔ tứ giác $ADFC$ nội tiếp và $\angle DFE = 90^\circ$
Điều này xảy ra khi $AE$ vuông góc với $CD$ (vì CD ⊥ OA, nên khi AE ⊥ CD thì DF ⊥ AE)
Vì $CD \perp OA$, nên AE vuông góc CD ⇔ AE // OA ⇒ E nằm đối xứng với A qua trục CD ⇒ E là trung điểm của đoạn IC
Vậy:
Độ dài $DF$ đạt giá trị lớn nhất khi E là trung điểm của đoạn IC.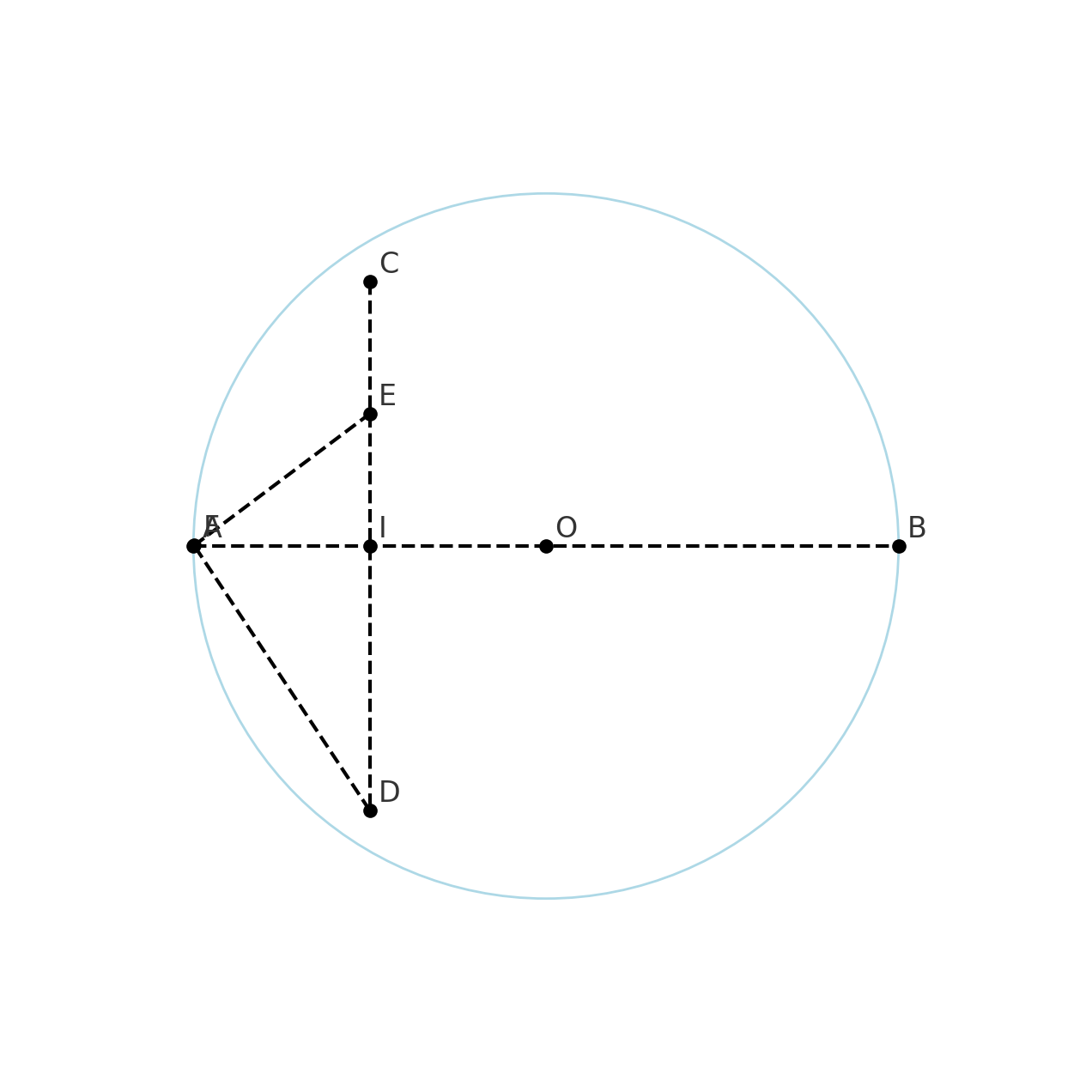
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


