Cho parabol(p) v y=x2 và đường thẳng d: y= -x+2
a) Vẽ parabol(p) và đường thẳng d trên hệ trục tọa độ.
b) Xác định tọa độ giao điểm của (p) và d bằng phép tính.
Quảng cáo
3 câu trả lời 172
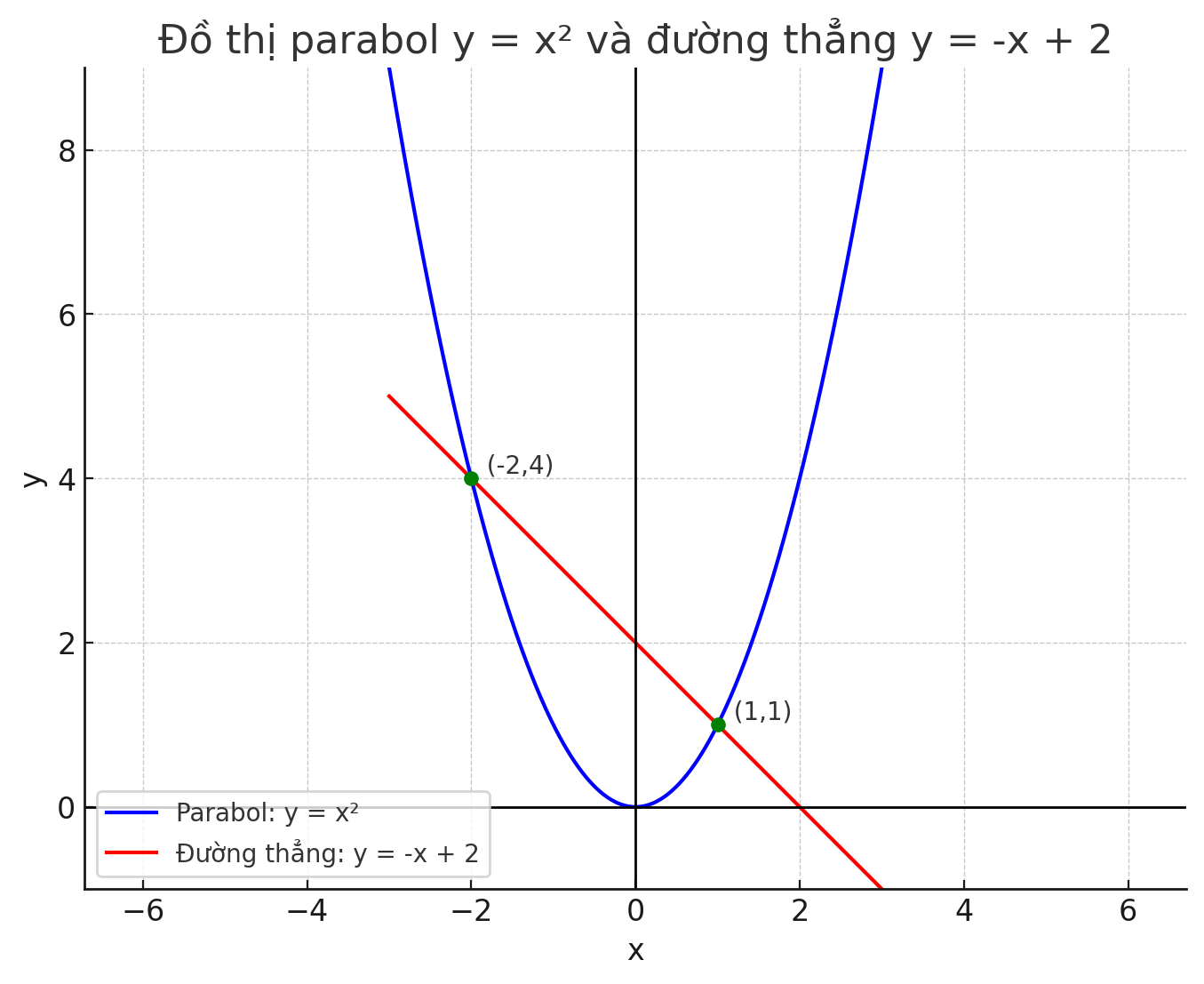
Ta tìm giao điểm của parabol và đường thẳng bằng cách giải hệ phương trình:
a)
Tập xác định: $D = \mathbb{R}$.
Parabol có đỉnh là $O(0,0)$, trục đối xứng là trục $Oy$.
Vì $a = 1 > 0$ nên parabol có bề lõm hướng lên trên.
Bảng giá trị:
| $x$ | -2 | -1 | 0 | 1 | 2 |
| :---- | :-: | :-: | :-: | :-: | :-: |
| $y=x^2$ | 4 | 1 | 0 | 1 | 4 |
Vẽ đường cong đi qua các điểm $(-2,4), (-1,1), (0,0), (1,1), (2,4)$.
Vẽ đường thẳng (d): $y = -x + 2$
Cho $x = 0 \Rightarrow y = 2$. Điểm $A(0,2)$.
Cho $y = 0 \Rightarrow -x + 2 = 0 \Rightarrow x = 2$. Điểm $B(2,0)$.
Vẽ đường thẳng đi qua hai điểm $A(0,2)$ và $B(2,0)$.
b)
Phương trình hoành độ giao điểm của (P) và (d) là:
$x^2 = -x + 2$
$x^2 + x - 2 = 0$
Phương trình có dạng $a+b+c = 1+1-2=0$ nên có hai nghiệm phân biệt:
$x_1 = 1$
$x_2 = \frac{c}{a} = \frac{-2}{1} = -2$
Với $x_1 = 1 \Rightarrow y_1 = 1^2 = 1$. Tọa độ giao điểm thứ nhất là $M(1,1)$.
Với $x_2 = -2 \Rightarrow y_2 = (-2)^2 = 4$. Tọa độ giao điểm thứ hai là $N(-2,4)$.
`->`Vậy tọa độ giao điểm của (P) và (d) là $M(1,1)$ và $N(-2,4)$.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


