Cho đường tròn tâm O và A thuộc (O) trên tiếp tuyến tại A của (O) lấy K Qua K vẽ đường thẳng d cắt (O) tại 2 điểm B và C ( d không đi qua O, B nằm giữa K và C) . Gọi M là trung điểm của BC . Vẽ đường kính AN . Đường thẳng đi qua A và vuông góc với BC cắt MN tại H Chứng minh CH vuông góc với AB
Quảng cáo
2 câu trả lời 120
Bài làm:
Vì A thuộc đường tròn (O), và tiếp tuyến tại A cắt đường tròn tại B, C sao cho B nằm giữa K và C, nên tam giác ABC là tam giác nội tiếp đường tròn (O), với AB và AC là các dây.
Gọi M là trung điểm của BC.
Vẽ đường kính AN ⇒ ∠ABN = ∠ACN = 90° (vì góc nội tiếp chắn nửa đường tròn).
Vẽ đường thẳng qua A vuông góc với BC, cắt đoạn MN tại H ⇒ ∠AHC = 90°
Xét tứ giác ABCH, ta có:
∠ABN = 90°
∠AHC = 90°
⇒ Tổng hai góc đối của tứ giác ABCH bằng 180° ⇒ ABCH nội tiếp
Mà tứ giác ABCH nội tiếp ⇒ ∠HCB = ∠HAB (cùng chắn cung AB)
→ Vì ∠HAB = 90° ⇒ ∠HCB = 90°
⇒ CH ⊥ AB
CH vuông góc với AB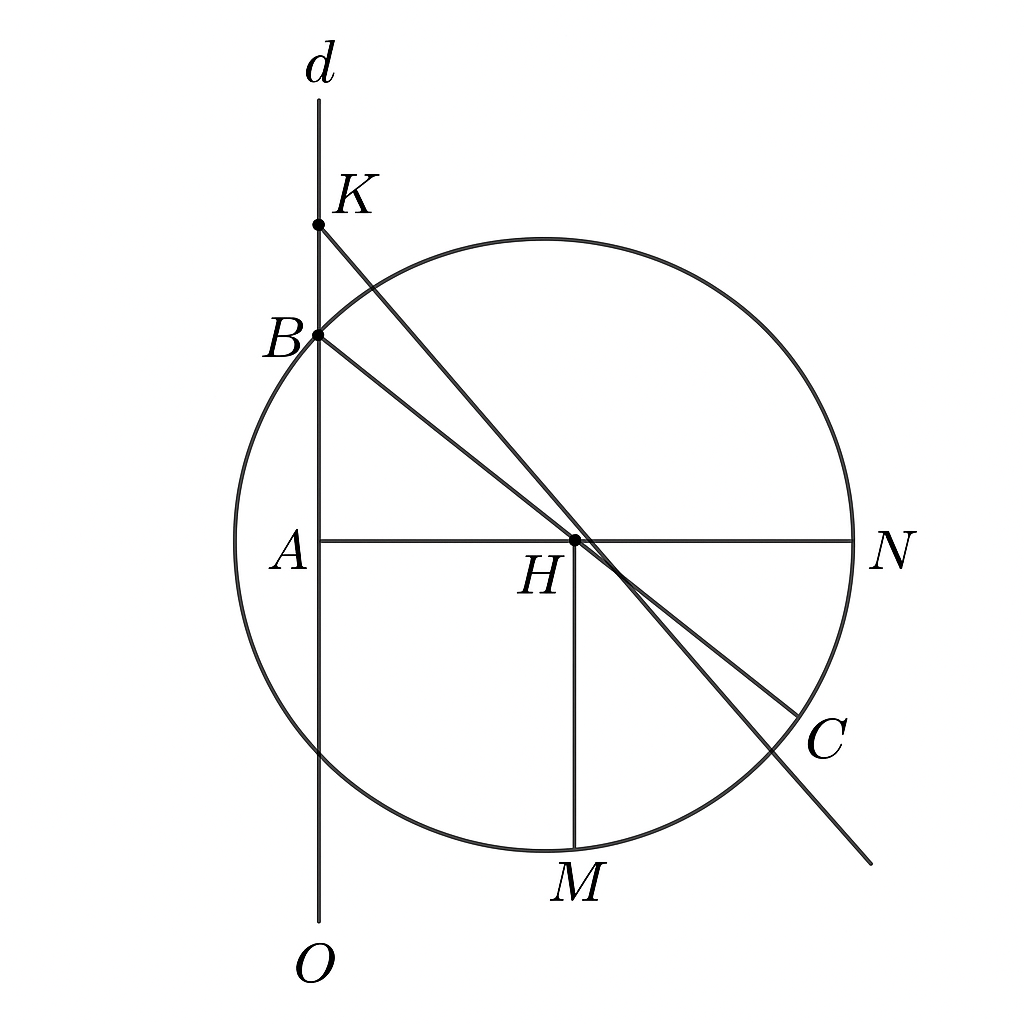
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387
Gửi báo cáo thành công!


