Quảng cáo
2 câu trả lời 406
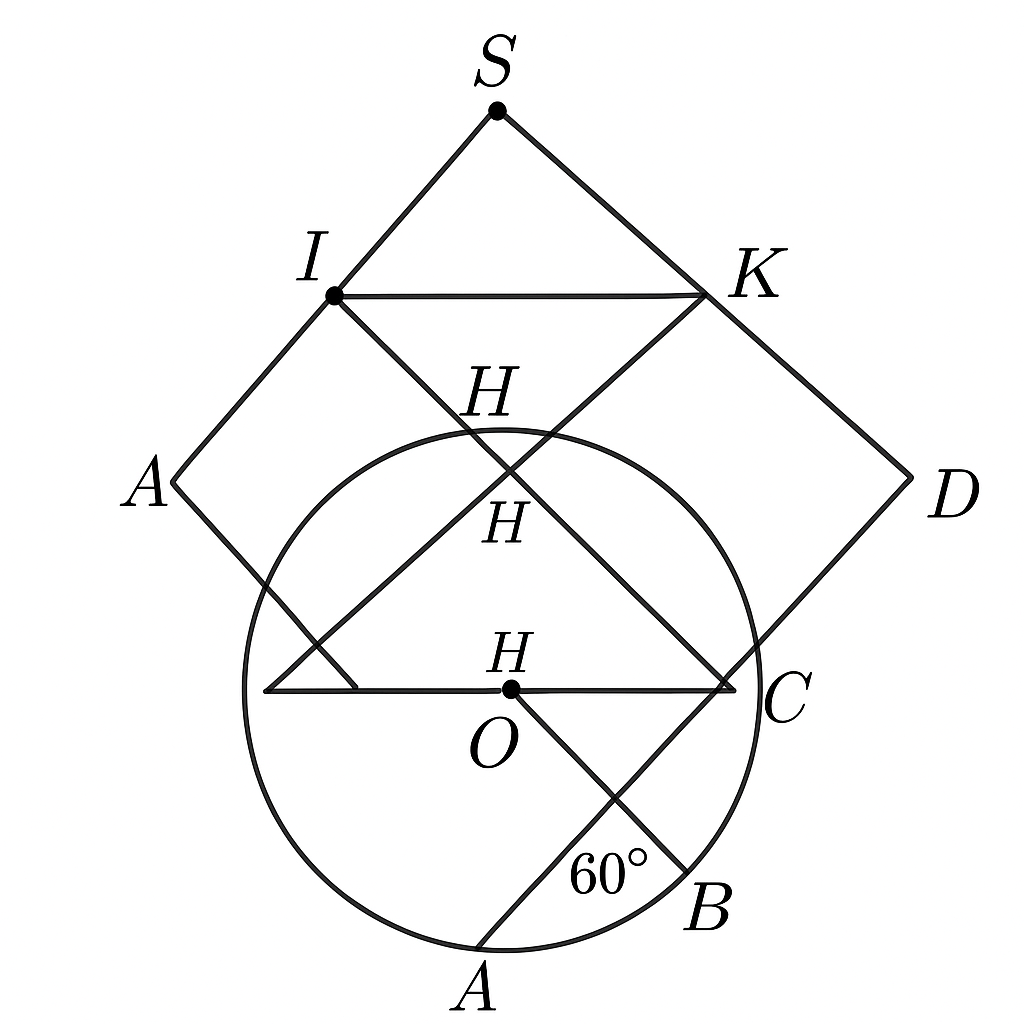
⇒ △ABCvuông tại A
⇒ △BDC vuông tại D
Ta biết:
H là giao điểm AC và BD
A,C∈(O), B,D∈(O)
∠SAH=∠CAB (góc trong tam giác ABCABCABC)
∠SDH=∠DCB (góc trong tam giác DBCDBCDBC)
Mà ∠CAB+∠DCB=180 vì là 2 góc trong cùng nửa đường tròn chắn BC
⇒ ∠SAH+∠SDH=180
⇒ Tứ giác SAHD nội tiếp
Ta có:
- I là trung điểm của SH
- K là giao điểm của DM và HC
Xét các góc tương ứng:
- ∠IAH=∠KDC
Vì các điểm cùng nằm trong các tam giác vuông △ABC và △BDC đã chứng minh ở câu a.
→ △IAH∼△KDC (góc – góc – cạnh tỉ lệ)
Dựa vào đối xứng, ta có thể suy ra:
- Tâm O nằm trung điểm BC, bán kính
- Giả sử góc ở tâm chắn cung AD là θ=60 (vì ∠BSC=60, giả thiết có thể đặt theo hình đối xứng)
Tính diện tích viên phân:
- Bán kính đường tròn:
-
Góc ở tâm θ=60
a) Chứng minh SH vuông góc với BC tại E và tứ giác HECD nội tiếp
Giả sử:
Bài toán cho nửa đường tròn (O) với đường kính BC. Trên nửa đường tròn (O), lấy hai điểm A và D theo thứ tự B, A, D, C. Tia BA và CD cắt nhau tại S, đoạn thẳng AC cắt BD tại H.OLM+1khoahoc.vietjack.com+1
Giải:
Do BC là đường kính của nửa đường tròn (O), theo định lý góc nội tiếp, ta có:OLM
∠BAC=∠BDC=90∘ \angle BAC = \angle BDC = 90^\circ∠BAC=∠BDC=90∘HOCMAI Forum
Từ đó, ta suy ra:OLM
CA⊥SB,BD⊥SC \text{CA} \perp \text{SB}, \quad \text{BD} \perp \text{SC}CA⊥SB,BD⊥SCOLM
Điều này chứng tỏ H là trực tâm của tam giác SBC.OLM
Vì SH là đường cao thứ ba của tam giác SBC, ta có:OLM
SH⊥BCtại E \text{SH} \perp \text{BC} \quad \text{tại E}SH⊥BCtại EOLM
Do đó, tứ giác HECD là tứ giác nội tiếp.OLM+1khoahoc.vietjack.com+1
b) Chứng minh góc TAH = góc KDC và suy ra CK·CA = CD·CI
Giả sử:
Gọi T là trung điểm của SH. Tia AT cắt SC tại I, DE cắt HC tại K.OLM+1khoahoc.vietjack.com+1
Giải:
Vì A và D cùng nhìn SH dưới một góc vuông, tứ giác SAHD nội tiếp đường tròn đường kính SH.OLM
Từ đó, ta suy ra:OLM
∠TAH=∠KDC \angle TAH = \angle KDC∠TAH=∠KDCOLM
Xét hai tam giác CKD và CIA có:OLM
∠KCD=∠KDC\angle KCD = \angle KDC∠KCD=∠KDC (chung)
∠KDC=∠TAH\angle KDC = \angle TAH∠KDC=∠TAH (từ trên)
Do đó, theo tiêu chí góc-góc-góc (g.g.g), ta có:
△CKD∼△CIA \triangle CKD \sim \triangle CIA△CKD∼△CIA
Từ đó, suy ra:
CKCI=CDCA⇒CK⋅CA=CD⋅CI \frac{CK}{CI} = \frac{CD}{CA} \quad \Rightarrow \quad CK \cdot CA = CD \cdot CICICK=CACD⇒CK⋅CA=CD⋅CIOLM
c) Chứng minh tam giác IAK cân
Giả sử:
Từ phần b), ta có △CKD∼△CIA\triangle CKD \sim \triangle CIA△CKD∼△CIA.
Do đó, ∠CKD=∠CIA\angle CKD = \angle CIA∠CKD=∠CIA.
Mặt khác, ∠CKD+∠AKD=180∘\angle CKD + \angle AKD = 180^\circ∠CKD+∠AKD=180∘ (góc kề bù).OLM
Tương tự, ∠CIA+∠AKD=180∘\angle CIA + \angle AKD = 180^\circ∠CIA+∠AKD=180∘.
Vì vậy, tứ giác AIDK là tứ giác nội tiếp.OLM+1khoahoc.vietjack.com+1
Do đó, ∠DAK=∠DIK\angle DAK = \angle DIK∠DAK=∠DIK (cùng chắn cung DK).OLM
Ngoài ra, D và E cùng nhìn SB dưới một góc vuông, nên tứ giác SBED là tứ giác nội tiếp.OLM
Từ đó, ∠DBC=∠DSE\angle DBC = \angle DSE∠DBC=∠DSE (cùng chắn cung DE).
Từ các quan hệ trên, ta có:
∠DAK=∠DIK \angle DAK = \angle DIK∠DAK=∠DIK
Điều này chứng tỏ tam giác IAK cân tại I
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


