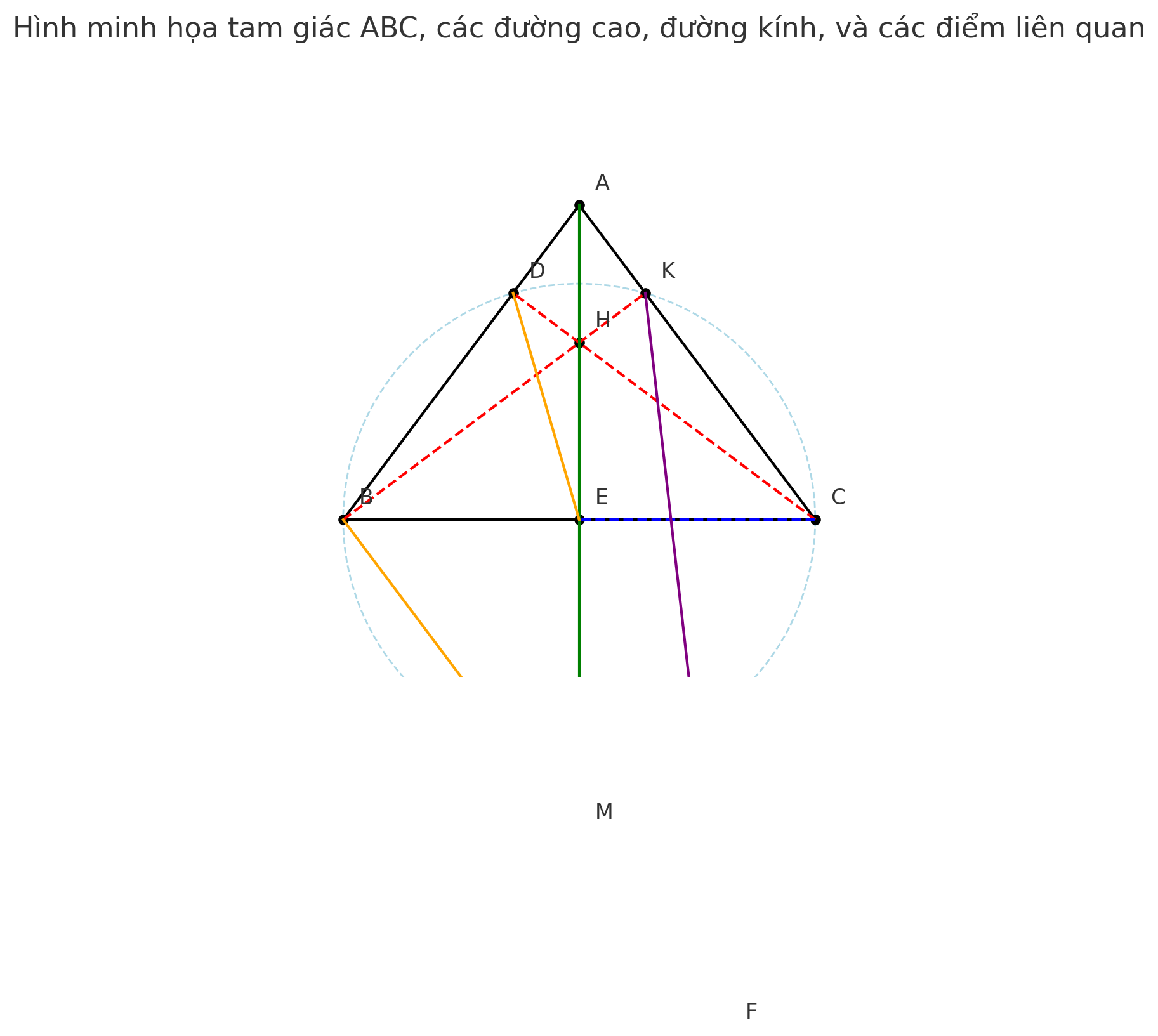
Cho tam giác ABC nhọn nội tiếp đường tròn (O) (AB<AC). Các đường cao CD (D thuộc AB) và BK (K thuộc AC) của tam giác ABC cắt nhau tại H. Vẽ đường kính AM, kẻ CE vuông góc với AM tại E.
a) Chứng minh tứ giác ADHK nội tiếp
b) Hai đường thẳng DE và BM cắt nhau tại F. Chừng minh DE.BC=DC.BM và KF // AM
giúp tớ với ạ
Quảng cáo
4 câu trả lời 1140
a) Chứng minh tứ giác ADHK nội tiếp
Ta sẽ chứng minh:
\[
\angle ADH + \angle AKH = 180^\circ
\]
- Vì CD ⊥ AB ⇒ \(\angle CDH = 90^\circ\)
- Vì BK ⊥ AC ⇒ \(\angle BKH = 90^\circ\)
Do đó, hai góc tại D và K trong tứ giác ADHK cùng bằng 90°, suy ra:
\[
\angle ADH + \angle AKH = 180^\circ
\Rightarrow \text{Tứ giác } ADHK \text{ nội tiếp}
\]
Tứ giác ADHK nội tiếp đường tròn.
b) Hai phần:
1) Chứng minh \( DE \cdot BC = DC \cdot BM \)
Xét các tam giác vuông có chung góc và sử dụng đồng dạng:
- Tam giác CDE vuông tại E
- Tam giác CBM vuông tại B (vì AM là đường kính, tam giác AMC vuông tại C ⇒ tam giác CBM cũng có góc vuông tại B)
Xét tam giác CDE và CBM, cùng góc tại C ⇒ đồng dạng:
\[
\triangle CDE \sim \triangle CBM \Rightarrow \frac{DE}{BM} = \frac{DC}{BC} \Rightarrow DE \cdot BC = DC \cdot BM
\]
\( \boxed{DE \cdot BC = DC \cdot BM} \)
2) Chứng minh \( KF \parallel AM \).
- Ta đã biết:
- KF ⊥ AC (vì K là chân đường cao từ B xuống AC)
- AM ⊥ AC (vì AM là đường kính, tam giác AMC vuông tại C)
⇒ KF và AM cùng vuông góc với AC ⇒ KF // AM
\( \boxed{KF \parallel AM} \)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


