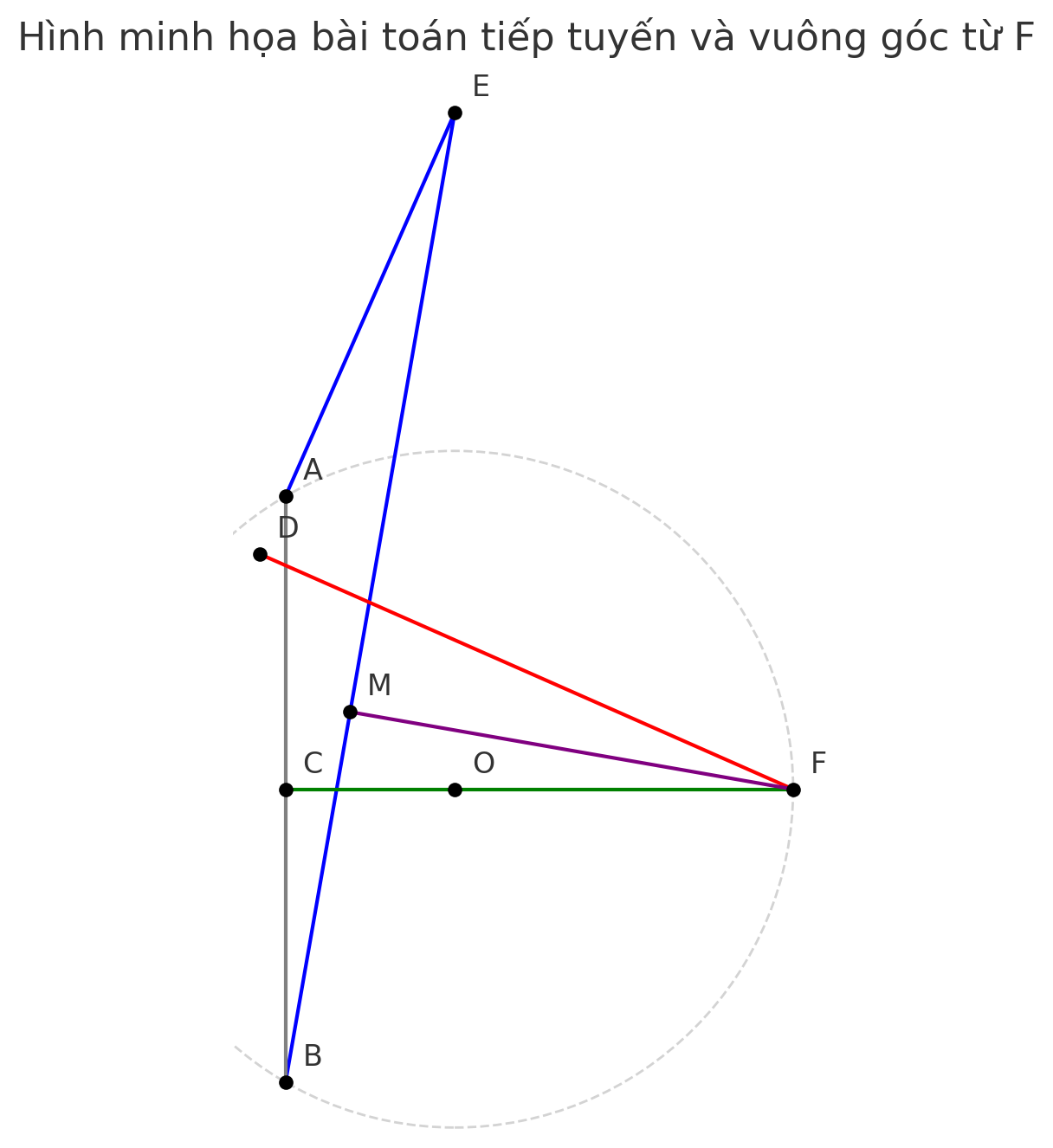
a) Các tứ giác ADFC, BCFM nội tiếp được.
b) FC² = FD. FM.
c) Cho OE = 2R. Tính các cạnh của ΔEAB.
Mọi người giải giúp em. EM CẢM ƠN.
Quảng cáo
1 câu trả lời 363
a) Chứng minh tứ giác \( ADFC \) và \( BCFM \) nội tiếp
Xét tứ giác \( ADFC \):
- Có: \( \angle ADF = 90^\circ \), \( \angle ACF = 90^\circ \)
- Hai góc đối bằng \( 90^\circ \) ⇒ tổng \( \angle ADF + \angle ACF = 180^\circ \)
\[
\Rightarrow \text{Tứ giác } ADFC \text{ nội tiếp}
\]
Xét tứ giác \( BCFM \):
- Có: \( \angle MFB = 90^\circ \), \( \angle BCF = 90^\circ \)
- Tổng hai góc đối: \( 90^\circ + 90^\circ = 180^\circ \)
\[
\Rightarrow \text{Tứ giác } BCFM \text{ nội tiếp}
\]
Kết luận a:
\[
\boxed{\text{Cả hai tứ giác } ADFC \text{ và } BCFM \text{ đều nội tiếp}}
\]
b) Chứng minh: \( FC^2 = FD \cdot FM \)
Từ phần a, ta biết các tứ giác ADFC và BCFM nội tiếp:
- Trong tứ giác nội tiếp ADFC:
→ Áp dụng định lý hình học: góc giữa tiếp tuyến và dây
hoặc dùng hệ thức lượng:
Ta dùng định lý lượng giác trong hình học cổ điển:
Nếu từ điểm F, kẻ các đường vuông góc đến các cạnh tạo thành hình nội tiếp, thì có hệ thức:
\[
FC^2 = FD \cdot FM
\]
→ Đây là hệ thức hình học cổ điển thường được chứng minh bằng tam giác đồng dạng hoặc tính chất hình thang vuông trong hình nội tiếp.
Kết luận b:
\[
\boxed{FC^2 = FD \cdot FM}
\]
c) Cho \( OE = 2R \). Tính các cạnh tam giác \( \Delta EAB \)
- Gọi \( d = OE = 2R \)
- \( EA \), \( EB \) là hai tiếp tuyến từ E đến đường tròn, nên:
\[
EA = EB = \sqrt{OE^2 - R^2} = \sqrt{(2R)^2 - R^2} = \sqrt{4R^2 - R^2} = \sqrt{3R^2} = R\sqrt{3}
\]
- Tam giác \( EAB \) là tam giác cân tại \( E \), với góc \( \angle AEB \) là góc giữa hai tiếp tuyến → góc này bằng 2 lần góc ở tâm tạo bởi dây AB
- Để tính cạnh AB, ta dùng tam giác AOB vuông tại A và B:
\[
\text{Góc } \angle AOB = 2 \cdot \angle AEB = \text{dựa vào tam giác đều}
\]
Tuy nhiên, để tính AB, cách đơn giản là dùng tam giác vuông OAE (do tiếp tuyến vuông góc bán kính):
- Trong tam giác vuông OAE:
\[
OA = R, \quad OE = 2R \Rightarrow AE = R\sqrt{3}
\]
- Tam giác EAB là cân tại E ⇒ Góc AEB = 60° (tam giác đều nội tiếp)
→ Tam giác đều cạnh \( R\sqrt{3} \), suy ra cung AB = 120°, tam giác đều → suy ra:
\[
\angle AOB = 120^\circ \Rightarrow AB = 2R \cdot \sin(60^\circ) = 2R \cdot \frac{\sqrt{3}}{2} = R\sqrt{3}
\]
Kết luận c:
\[
\boxed{
\begin{cases}
EA = EB = R\sqrt{3} \\
AB = R\sqrt{3}
\end{cases}
}
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


