Question

Đã trả lời bởi chuyên gia

Answer 1

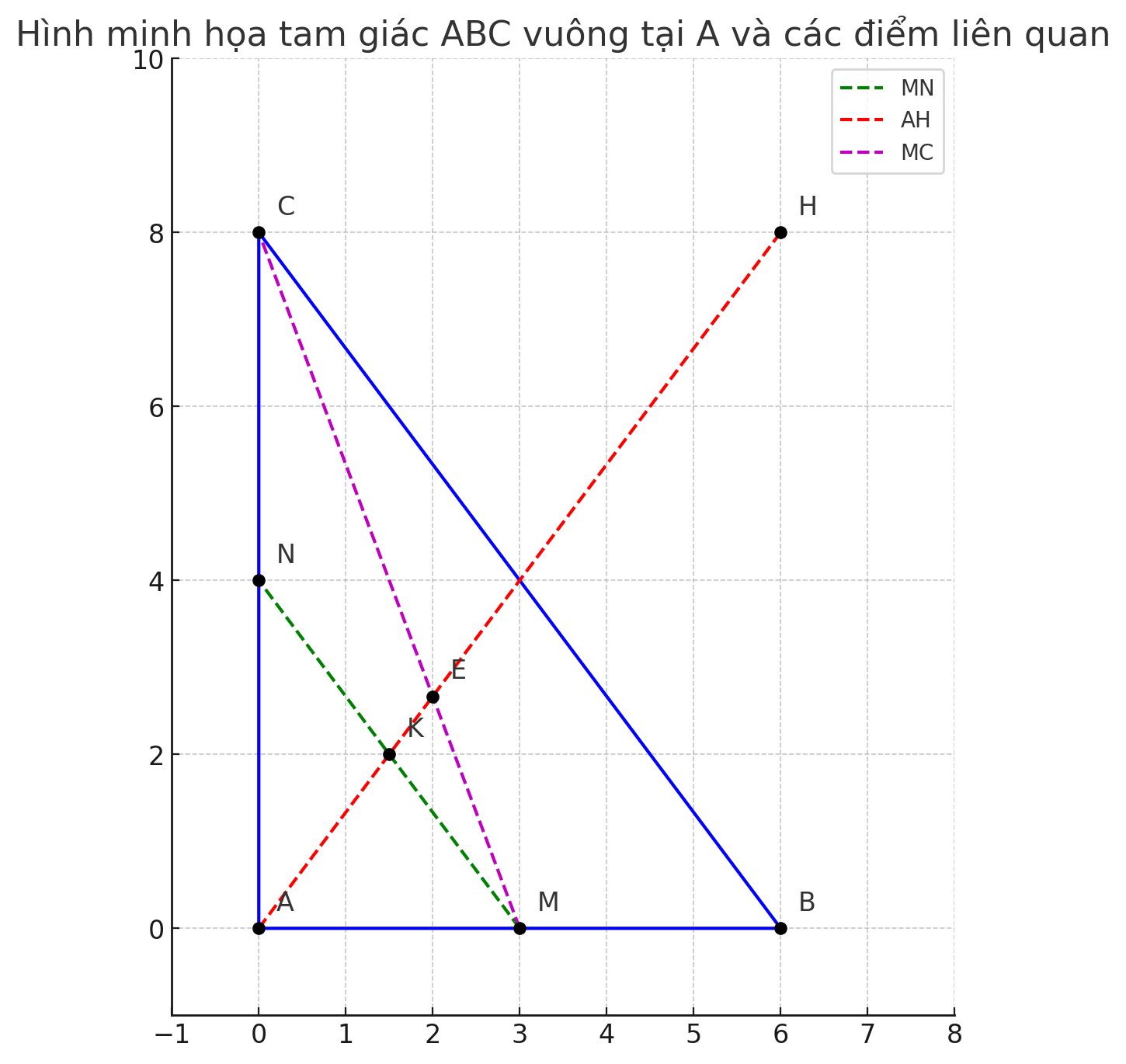
Vì \( M, N \) là trung điểm \( AB \) và \( AC \), nên \( MN \) là đường trung bình trong tam giác \( ABC \).
- Theo tính chất đường trung bình:
\[
MN \parallel BC \quad \text{và} \quad MN = \frac{1}{2} BC
\]
- \( AH \perp BC \) (vì \( AH \) là đường cao hạ từ đỉnh góc vuông).

→ \( AH \perp MN \) (vì \( MN \parallel BC \)).

- \( AH \perp MN \)
- \( MC \) cắt \( AH \) tại \( E \).

Xét các tam giác đồng dạng

- Tam giác \( AMC \) vuông tại \( M \) vì \( M \) là trung điểm \( AB \) và \( A \) vuông → \( AMC \) cũng vuông tại \( M \).
- \( D \) là hình chiếu vuông góc của \( A \) lên \( MC \), nên:
- \( AD \perp MC \).

Trong tam giác vuông, theo tính chất hình chiếu, ta có:

Hệ thức lượng trong tam giác vuông:
\[
MD \times MC = ME^2
\]

Nhưng đề bài yêu cầu chứng minh liên quan đến tổng nghịch đảo, nên mình sẽ phải dùng biến đổi khác.

Dùng tỉ số đoạn thẳng

Xét tam giác vuông \( AMC \) có đường cao \( AD \) (từ góc vuông hạ xuống cạnh huyền \( MC \)):

Áp dụng hệ thức lượng:
\[
AD^2 = MD \times MC
\]

(1) Ngoài ra vì \( E \) là giao điểm \( MC \) và \( AH \), mà \( AH \perp BC \), ta có trong tam giác vuông:
\[
ME \times MC = MA^2
\]

Nhưng vì \( M \) là trung điểm, nên \( MA = \frac{1}{2} AB \).
Cụ thể ta cần xác định dựa trên độ dài thực tế hoặc dùng tỉ số.

Cách chứng minh đúng

Trong tam giác \( AMC \), vuông tại \( M \):

Áp dụng hệ thức lượng:
\[
\frac{1}{MD} + \frac{1}{MC} = \frac{MC + MD}{MD \times MC}
\]

Từ đó:

- Theo hệ thức lượng:
\[
MD \times MC = ME \times ME = ME^2
\]
(Do E là chân đường cao từ \( M \) trong tam giác vuông).

Nên:

\[
\frac{MC + MD}{ME^2}
\]

---

Vậy ta cần chứng minh:
\[
\frac{MC + MD}{ME^2} = \frac{2}{ME}
\]

Tức là:
\[
MC + MD = 2ME
\]

→ Đây là điều cần chứng minh tiếp.

...Xem thêm

Answer 2