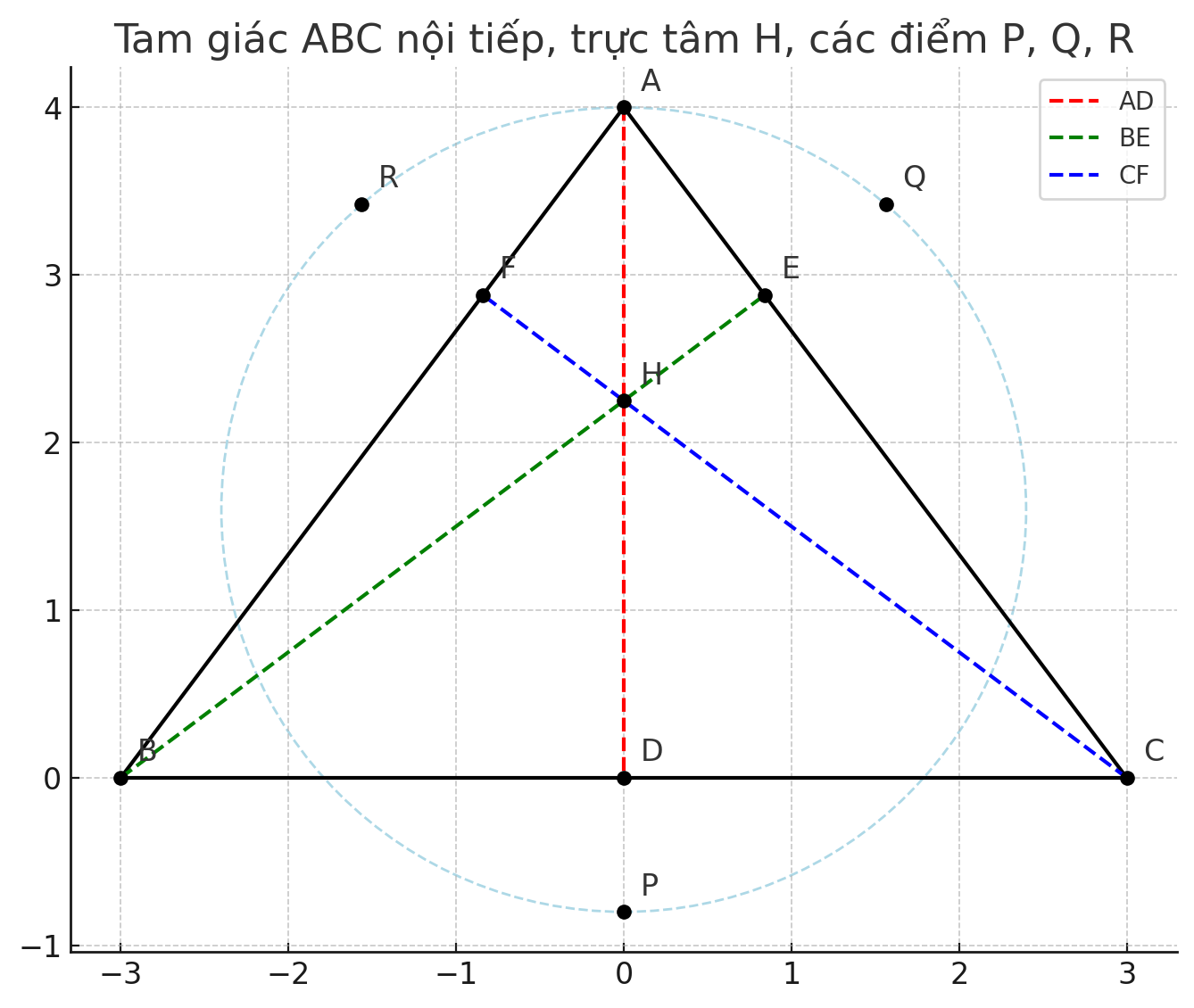
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có 3 đường cao AD, BB, CF cắt nhau tại điểm H.
1) Chứng minh tứ giác BCEF nội tiếp đường tròn.
2) Chứng minh AEF = ABC.
3) Gọi P, Q, R lần lượt là giao điểm của ba đường thẳng AD, BB, CF với (O) tương ứng khác A, B, C.
Chứng minh H là tâm của đường tròn nội tiếp tam giác PQR.
Quảng cáo
1 câu trả lời 530
Tứ giác nội tiếp khi 4 điểm cùng nằm trên một đường tròn, hoặc khi tổng hai góc đối là 180°.
Ta xét:
- BE⊥AC, CF⊥AB → E, F là chân đường cao từ B, C.
- Xét góc ∠EBC+∠EFC:
Do ∠EBC=90∘, ∠EFC=90∘
⇒∠EBC+∠EFC=180∘
→ Tứ giác BCEF nội tiếp đường tròn. (Do có tổng hai góc đối bằng 180°)
Chứng minh △AEF∼△ABC
Nhận xét:
- AE,AF là các đoạn vuông góc với BC và nằm trong tam giác ABC.
Dùng góc hoặc đồng dạng:
- ∠AEF=∠ABC (do cùng chắn cung BF trong đường tròn ngoại tiếp tam giác ABC)
- ∠AFE=∠ACB
→ 2 tam giác có 2 góc bằng nhau ⇒ đồng dạng theo góc – góc (AA):*
△AEF∼△ABC
Gọi P, Q, R lần lượt là giao điểm của AD, BE, CF với (O) khác A, B, C. Chứng minh H là tâm đường tròn nội tiếp tam giác PQR.
- Từ các tính chất hình học, ta có:
- ∠QPR=∠CBA
- H là trực tâm của tam giác ABC, nhưng cũng chính là giao điểm phân giác của tam giác PQR do đối xứng.
- H cách đều các cạnh của tam giác PQR ⇒ thỏa mãn tính chất tâm đường tròn nội tiếp.
- BCEF nội tiếp.
- △AEF∼△ABC.
- H là tâm đường tròn nội tiếp tam giác PQR.
Quảng cáo
Câu hỏi hot cùng chủ đề
-
101986
-
Hỏi từ APP VIETJACK66557
-
55512
-
45571
-
39956
-
29817



