1) Để chuẩn bị tham gia kì thi tuyển sinh vào lớp 10 đạt kết quả như mong đợi, bạn Dũng đã lập kế hoạch sẽ làm xong 80 bài tập trong khoảng thời gian nhất định với số lượng bài tập được chia đều trong các ngày. Trên thực tế, khi làm bài tập mỗi ngày bạn Dũng đã làm thêm 2 bài tập so với kế hoạch ban đầu nên đã hoàn thành sớm hơn 2 ngày so với dự định. Hỏi theo kế hoạch, mỗi ngày bạn Ding phải làm xong bao nhiêu bài tập? 2) Cho tam giác vuông ABC vuông tại AB = 3a, AC = 4a, với 0< a e R. Tính theo a diện tích toàn phần và thể tích của hình nón tạo thành khi quay tam giác vuông ABC quanh đường thẳng AC.

tutai17042010@icloud.com Hỏi từ APP VIETJACK

· 22:19 23/04/2025

1) Để chuẩn bị tham gia kì thi tuyển sinh vào lớp 10 đạt kết quả như mong đợi, bạn Dũng đã lập kế hoạch sẽ làm xong 80 bài tập trong khoảng thời gian nhất định với số lượng bài tập được chia đều trong các ngày. Trên thực tế, khi làm bài tập mỗi ngày bạn Dũng đã làm thêm 2 bài tập so với kế hoạch ban đầu nên đã hoàn thành sớm hơn 2 ngày so với dự định. Hỏi theo kế hoạch, mỗi ngày bạn Ding phải làm xong bao nhiêu bài tập?
2) Cho tam giác vuông ABC vuông tại AB = 3a, AC = 4a, với 0< a e R. Tính theo a diện tích toàn phần và thể tích của hình nón tạo thành khi quay tam giác vuông ABC quanh đường thẳng AC.

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

1 câu trả lời 219

Chinh nè

2 tháng trước

Giả sử kế hoạch ban đầu là làm xong 80 bài tập trong $x$ ngày.
⇒ Mỗi ngày Dũng dự định làm:
$\frac{80}{x} \text{ bài tập}$

Trên thực tế, mỗi ngày làm thêm 2 bài ⇒ mỗi ngày làm:
$\frac{80}{x} + 2 \text{ bài tập}$

Do làm nhiều hơn nên Dũng hoàn thành sớm hơn 2 ngày ⇒ thời gian thực tế là $x - 2$ ngày.

Ta có phương trình:
$\left(\frac{80}{x} + 2\right)(x - 2) = 80$

Rút gọn:
$\frac{80(x - 2)}{x} + 2(x - 2) = 80$

$\frac{80(x - 2)}{x} + 2(x - 2) = 80 \\ \Rightarrow \frac{80(x - 2)}{x} + 2x - 4 = 80$

Nhân cả hai vế với $x$ để khử mẫu:
$80(x - 2) + x(2x - 4) = 80x \Rightarrow 80x - 160 + 2x^2 - 4x = 80x \Rightarrow 2x^2 - 4x - 160 = 0 \Rightarrow x^2 - 2x - 80 = 0$

Giải phương trình:
$x = \frac{2 \pm \sqrt{4 + 4 \cdot 80}}{2} = \frac{2 \pm \sqrt{324}}{2} = \frac{2 \pm 18}{2} \Rightarrow x = 10 \text{ (loại nghiệm âm)}$

⇒ Mỗi ngày theo kế hoạch bạn Dũng làm:
$\frac{80}{10} = \boxed{8 \text{ bài tập}}$

---

Bài 2: Thể tích và diện tích toàn phần của hình nón

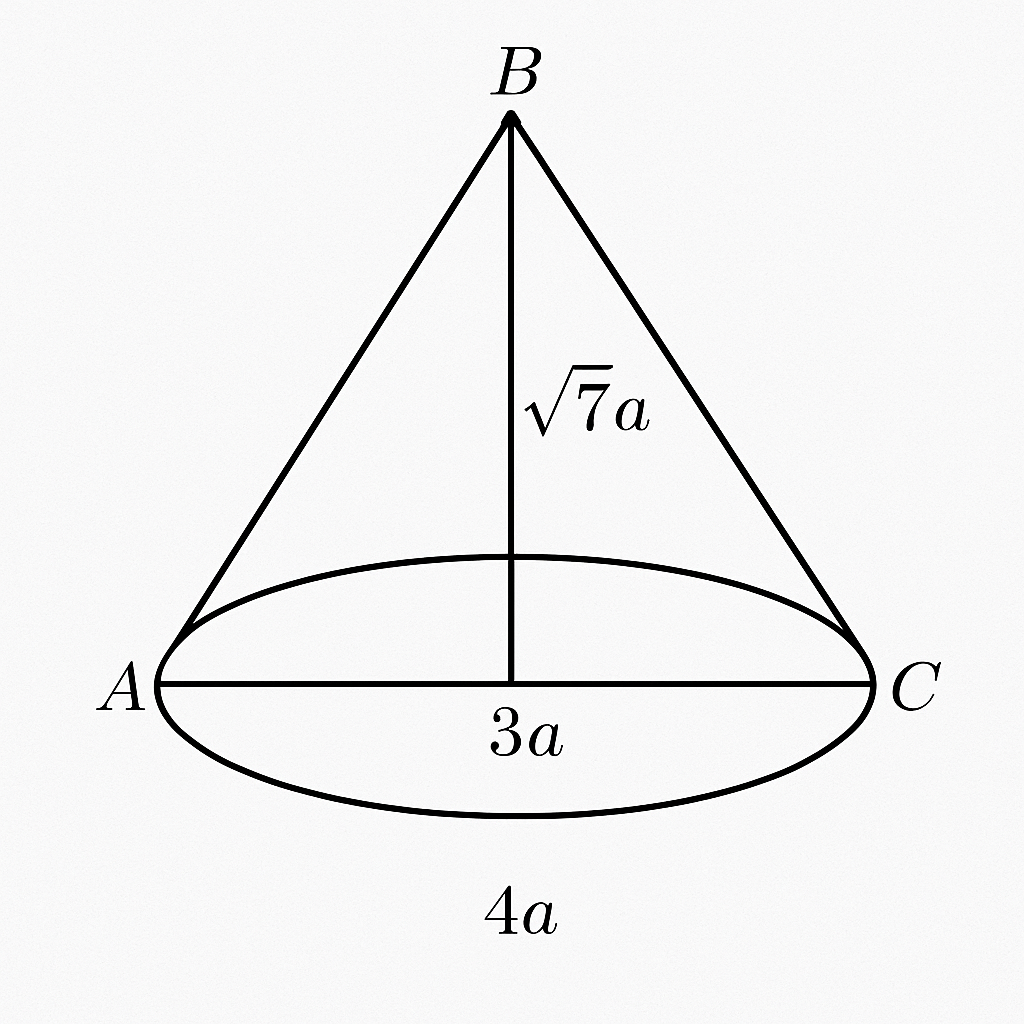
Cho tam giác vuông ABC vuông tại B, với:
- AB = 3a
- AC = 4a (đường quay)
⇒ Theo định lý Pythagoras:
$BC = \sqrt{AC^2 - AB^2} = \sqrt{(4a)^2 - (3a)^2} = \sqrt{16a^2 - 9a^2} = \sqrt{7}a$

Ta tính chiều cao (h) bằng công thức khoảng cách từ điểm đến đường thẳng:

Diện tích tam giác ABC:
$S = \frac{1}{2} \cdot AB \cdot BC = \frac{1}{2} \cdot 3a \cdot \sqrt{7}a = \frac{3\sqrt{7}}{2}a^2$

Chiều cao từ B đến AC là:
$h = \frac{2S}{AC} = \frac{2 \cdot \frac{3\sqrt{7}}{2}a^2}{4a} = \frac{3\sqrt{7}a}{4}$

Thể tích hình nón:
$V = \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi \left(\frac{3\sqrt{7}a}{4}\right)^2 \cdot 4a \\ = \frac{1}{3} \pi \cdot \frac{189a^2}{16} \cdot 4a = \frac{1}{3} \pi \cdot \frac{756a^3}{16} = \frac{252\pi a^3}{16} = \boxed{\frac{63\pi a^3}{4}}$

Độ dài đường sinh (l): chính là cạnh AB = 3a
Bán kính đáy (r) = chiều cao = $\frac{3\sqrt{7}a}{4}$

Diện tích xung quanh:
$S_{xq} = \pi r l = \pi \cdot \frac{3\sqrt{7}a}{4} \cdot 3a = \frac{9\pi \sqrt{7}a^2}{4}$

Diện tích đáy:
$S_{đáy} = \pi r^2 = \pi \cdot \left(\frac{3\sqrt{7}a}{4}\right)^2 = \frac{63\pi a^2}{16}$

Tổng diện tích toàn phần:
$S_{tp} = S_{xq} + S_{đáy} = \frac{9\pi \sqrt{7}a^2}{4} + \frac{63\pi a^2}{16} = \pi a^2 \left( \frac{9\sqrt{7}}{4} + \frac{63}{16} \right)$

Quy đồng mẫu:
$= \pi a^2 \left( \frac{36\sqrt{7} + 63}{16} \right) = \boxed{\pi a^2 \cdot \frac{36\sqrt{7} + 63}{16}}$

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

1 câu trả lời 219

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 9